Дифракция Френеля на круглом отверстии

Рассмотрим падение сферической волны, распространяющейся в изотропной однородной среде от точечного источника , на непрозрачный экран с круглым отверстием радиуса (диафрагмой). Точка наблюдения расположена против центра отверстия. Обозначим через 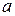– расстояние от источника до волновой поверхности, b – расстояние от волновой поверхности до точки наблюдения (рис.6а).

Открытую для точки наблюдения часть волновой поверхности разобьем на зоны, называемые зонами Френеля (см. выше).

Выражение для определения радиуса внешней границы m -ой зоны Френеля было получено выше: .

Если при заданных a и b выполняется равенство, что , то отверстие оставляет открытым m зон Френеля, которое равняется: .

Таким образом, при заданных длине световой волны, размерах отверстия и расстояниях от источника до точки наблюдения можно определить число зон Френеля, создающих колебания в т. , при этом амплитуда результирующего колебания будет определяться:

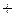, где «» соответствует нечётному значению m, «–» – чётному.

а) При чётном m последнее выражение можно переписать в следующем виде:

Приближённо полагая слагаемые в скобках равными нулю, получаем, что результирующее колебание в точке наблюдения: , где – целое чётное число.

б) При нечётном m амплитуду колебаний в точке P можно записать в следующем виде:

.

Приближённо полагая слагаемые в скобках равными нулю, получаем, что результирующее колебание в точке наблюдения: , где – целое нечётное число.

Поскольку амплитуды полей, излучаемых соседними зонами Френеля, практически одинаковые, в общем случае результирующее колебание в т. можно записать в виде:

, (4)

где – «–» соответствует случаю, когда открытым является чётное количество зон Френеля, «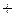» – нечётное.

Поскольку при малых значениях амплитуды колебаний, возбуждаемых в т. соседними зонами Френеля, практически одинаковые и равны , то результирующее колебание в т. согласно (4) при чётном – , нечётном –

Таким образом, при нечётном диафрагма увеличивает интенсивность света в точке наблюдения в четыре раза по сравнению со случаем, когда диафрагма отсутствует, при чётном – интенсивность приблизительно равна нулю (можно сравнить данный результат с результатом, полученным из векторной диаграммы).

Интенсивность световой волны на экране в зависимости от положения точки наблюдения можно качественно определить пользуясь методом зон Френеля. Рассмотрим сферическую волну, падающую на непрозрачный экран, в котором имеется отверстие, открывающее для точки наблюдения зон Френеля, число которых нечетное (рис.6б). Для т. , расположенной несимметрично, “сверху” закрывается часть последней -ой зоны Френеля (которая, создает колебание в т. в фазе с колебанием, создаваемым в т. , первой зоной) и открывается “снизу” часть 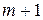зоны Френеля (которая, создает колебания в т. в противофазе с первой зоной). В результате интенсивность в т. меньше по сравнению с интенсивностью в т. . Интенсивность будет уменьшается до тех пор, пока -ая зона для т. не закроется полностью и не откроется 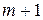зона. При дальнейшем смещении т. “сверху” закрывается часть зоны, а “снизу” открывается часть зоны. Колебание, которое создает в т. зона находится в фазе с первой зоной и интенсивность в т. увеличивается и т.д.

Таким образом, при перемещении точки в радиальном направлении мы проходим последовательность максимумов и минимумов интенсивности. Дифракционная картина представляет собой чередование светлых и тёмных колец на экране. При нечётном m – в центре светлое пятно, при чётном – тёмное. Если отверстие в экране открывает лишь часть первой зоны Френеля, на экране получается размытое светлое пятно. Если отверстие открывает большое число зон Френеля, чередование светлых и тёмных колец наблюдается только в узкой границе, прилегающей к границе геометрической тени.

Поиск по сайту: