 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракция Френеля. В случае дифракции Френеля вычисление интенсивности на дифракционной картине без проведения трудоемких численных расчетов возможно лишь в некоторых простейших
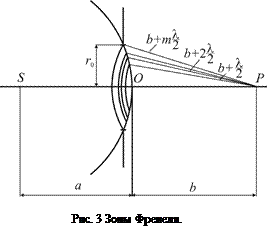
В случае дифракции Френеля вычисление интенсивности на дифракционной картине без проведения трудоемких численных расчетов возможно лишь в некоторых простейших случаях. В частности, при дифракции на круглом отверстии или диске используется метод, основанный на построении зон Френеля. Волновая поверхность сферической волны от точечного источника 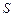 , проходящая через точку
, проходящая через точку 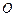 , разбивается на кольцевые зоны (рис. 3). Расстояние от точки наблюдения
, разбивается на кольцевые зоны (рис. 3). Расстояние от точки наблюдения 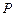 до границ этих зон увеличивается с шагом
до границ этих зон увеличивается с шагом 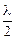 , начиная от минимального значения
, начиная от минимального значения 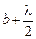 , где
, где 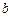 - расстояние между точками
- расстояние между точками 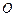 и
и 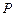 . Если рассматривать не очень большое число кольцевых зон, то при таком построении их площади оказываются практически одинаковыми, а радиус
. Если рассматривать не очень большое число кольцевых зон, то при таком построении их площади оказываются практически одинаковыми, а радиус 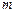 -ой зоны определяется выражением
-ой зоны определяется выражением
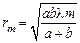 . (6)
. (6)
Согласно принципу Гюйгенса – Френеля множество точек волновой поверхности в пределах каждой зоны возбуждает в точке 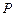 колебание. Из условий построения следует, что фазы колебаний, возбуждаемых соседними зонами Френеля, отличаются друг от друга на
колебание. Из условий построения следует, что фазы колебаний, возбуждаемых соседними зонами Френеля, отличаются друг от друга на 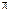 . Амплитуды же возбуждаемых колебаний
. Амплитуды же возбуждаемых колебаний 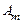 уменьшаются с ростом номера зоны
уменьшаются с ростом номера зоны 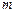 , так как постепенно увеличивается расстояние
, так как постепенно увеличивается расстояние  от
от 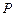 до
до 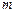 -ой зоны и становится меньше множитель
-ой зоны и становится меньше множитель 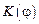 из-за возрастания угла
из-за возрастания угла 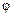 , т.е. справедливо соотношение
, т.е. справедливо соотношение
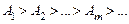 (7)
(7)
 |
С учетом сдвига фаз на
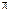 между колебаниями от соседних зон для амплитуды результирующего колебания получим
между колебаниями от соседних зон для амплитуды результирующего колебания получим

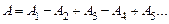 (8)
(8)
Используя (7) и (8) можно вычислить амплитуду колебания в точке 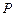 при дифракции на круглом отверстии или диске. Отверстие радиусом
при дифракции на круглом отверстии или диске. Отверстие радиусом 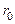 отрывает для точки
отрывает для точки 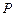 число зон Френеля, равное
число зон Френеля, равное
 . (9)
. (9)
Тогда, при нечетных 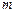
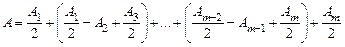 , (10)
, (10)
а при четных 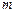
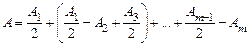 . (11)
. (11)
Так как в приведенных формулах выражения в скобках приблизительно равны нулю, то при нечетных 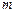 амплитуда результирующего колебания равна
амплитуда результирующего колебания равна 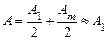 в то время как для четных
в то время как для четных 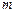 она близка к нулю.
она близка к нулю.
Амплитуду колебаний, возбуждаемых вторичными сферическими волнами в точке 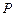 , можно также найти, используя графический метод. Для этого сферическая волновая поверхность разбивается на узкие кольцевые зоны, расстояние от границ которых до
, можно также найти, используя графический метод. Для этого сферическая волновая поверхность разбивается на узкие кольцевые зоны, расстояние от границ которых до 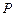 увеличивается на постоянную величину
увеличивается на постоянную величину 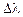 . Площади этих зон, как и зон Френеля, являются примерно одинаковыми, возбуждаемые ими колебания сдвинуты по фазе на одинаковую величину
. Площади этих зон, как и зон Френеля, являются примерно одинаковыми, возбуждаемые ими колебания сдвинуты по фазе на одинаковую величину 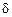 , а их амплитуда уменьшается по мере удаления зоны от вершины волновой поверхности. Тогда, используя комплексную форму записи, для результирующего колебания в точке
, а их амплитуда уменьшается по мере удаления зоны от вершины волновой поверхности. Тогда, используя комплексную форму записи, для результирующего колебания в точке 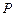 имеем
имеем
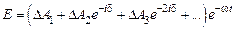 (12)
(12)
где 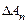 - амплитуда колебания, возбуждаемого
- амплитуда колебания, возбуждаемого 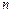 -ой узкой кольцевой зоной.
-ой узкой кольцевой зоной.
Представим каждое из слагаемых в скобках выражения (12) в виде вектора на комплексной плоскости и условимся отрицательный сдвиг фазы обозначать поворотом против часовой стрелки. В результате получим векторную диаграмму, показанную на рис. 4, которая называется спиралью Френеля. Амплитуда результирующего колебания определяется модулем суммы векторов. По мере увеличения числа зон результирующий вектор описывает своим концом спираль, которая в случае полностью открытой волновой поверхности сходится к точке 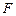 , и при этом амплитуда колебания в точке
, и при этом амплитуда колебания в точке 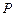 равна
равна  . На рис. 4 также показаны положения конца результирующего вектора при открытой первой, второй и т.д. зонах Френеля.
. На рис. 4 также показаны положения конца результирующего вектора при открытой первой, второй и т.д. зонах Френеля.
Поиск по сайту: