 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
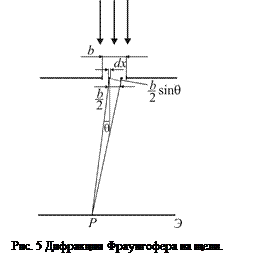
Дифракция Фраунгофера. Рассмотрим дифракцию света на экране с узкой щелью шириной в случае, для которого волновая поверхность плоской падающей волны и экран параллельны друг другу
Рассмотрим дифракцию света на экране с узкой щелью шириной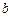 
в случае, для которого волновая поверхность плоской падающей волны и экран параллельны друг другу (рис. 5). Дифракцию Фраунгофера наблюдают на экране 
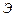, достаточно удаленном от щели для выполнения условия (4), и ее вид одинаков в любой плоскости, перпендикулярной щели.
 |
Для определения амплитуды колебания в точке
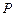на основе выражения (1) щель разбивается на узкие полосы шириной 
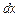. При вычислении интеграла принимается во внимание, что световые лучи, приходящие в 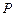от разных полос, почти параллельны друг другу, и тогда, распределение интенсивности можно представить в виде
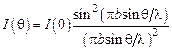, (13)
где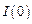 
и 
- интенсивность в центре дифракционной картины и в точке, положение которой определяется углом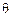 
.
График распределения интенсивности показан на рис. 6. В середине дифракционной картины располагается центральный максимум, на долю которого приходится большая часть интенсивности прошедшего через щель света и ширина которого обратно пропорциональна 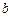. Кроме центрального максимума на картине наблюдается еще несколько максимумов небольшой интенсивности. Между ними располагаются минимумы, положение которых определяется условием
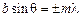, (14)
где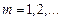 
 |
Возникновение центрального максимума связано с тем, что в центре дифракционной картины вторичные волны от всех узких полос в плоскости щели, проходя практически одинаковое расстояние, возбуждают колебания с почти одинаковыми фазами. Поэтому при
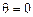интенсивность света принимает максимальное значение. При удалении от центра картины фазы колебаний, возбуждаемых вторичными сферическими волнами от узких полос, становятся разными в силу различий расстояний от точки на экране до источников этих волн. Поэтому амплитуда результирующего колебания постепенно уменьшается, становясь равной нулю при
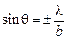. (15)
Появление каждого их этих минимумов легко понять, рассматривая колебания, которые возбуждают пары полос, удаленные друг от друга на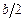 
(рис.5). При угле 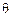, соответствующем минимуму, волны от любой пары таких полос приходят на экран в противофазе, поскольку их оптическая разность хода равна 
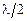, и гасят друг друга. Вследствие этого амплитуда результирующего колебания равна нулю. Возникновение последующих минимумов можно объяснить аналогичным образом, разбивая щель на множество пар полос, удаленных друг от друга или на 
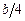, или на 
и т. д.
 |
Поиск по сайту: