 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Экономическая интерпретация задач линейного программирования
Пример. Пусть требуется определить план выпуска четырех видов продукции А, В, С, D, для изготовления которых используются ресурсы трех видов: трудовые, материальные, финансовые. Количество каждого i -го вида ресурса для производства каждого j -го вида продукции называют нормой расхода и обозначают аij. Количество каждого вида ресурса, которое имеется в наличии, обозначают bi (табл. 3).
Таблица 3
| Ресурсы (i) | Вид продукции (j) | Запас ресурса (bi) | |||
| А | В | С | D | ||
| Удельный расход ресурсов (аij) | |||||
| Трудовые | |||||
| Материальные | |||||
| Финансовые | |||||
| Граница нижняя | - | - | - | ||
| Граница верхняя | - | - | |||
| План | x1 | x2 | x3 | x4 | - |
Из табл. 3 видно, что для выпуска единицы продукции, например, вида А, требуется шесть единиц трудовых ресурсов, вида С - 11 единиц материальных ресурсов и т. д. Предприятие располагает 12000 единиц финансовых ресурсов, 2000 единиц материальных, 800 единиц трудовых. Исходя из рыночного спроса и производственно-технологических возможностей (производственной мощности, уровня специализации, минимальных объемов выпуска), заданы верхние и нижние предельные границы выпуска каждого вида продукции (в натуральных или стоимостных единицах).
Исходные данные таблицы по удельному расходу материальных и трудовых ресурсов проставляются в соответствии с действующей на предприятии нормативной и технологической документацией. Так, нормы расхода материальных ресурсов на каждое изготовляемое предприятием изделие содержатся в маршрутных ведомостях. Нормы трудоемкости изготовления изделия - в нормо-расценочных ведомостях или картах технологических процессов. Причем по строке «трудовые ресурсы» проставляется сводная трудоемкость изготовления изделия в нормо-часах как суммарная по всем деталеоперациям этого изделия. А по строке «материальные ресурсы» - норма расхода наиболее дефицитного (лимитируемого) вида материалов в принятых для этого материала единицах измерения (т, кг, м, л и др.). Впрочем, не исключена возможность представления всех исходных данных таблицы и в стоимостных единицах, как они проставлены по строке «финансовые ресурсы». Под удельным расходом финансовых ресурсов можно понимать, например, капиталоемкость производства каждого изделия, обусловленную необходимостью капитальных вложений в новое строительство или реконструкцию действующего производства. Если наличие каждого вида ресурсов (bi, i = 1, 2, 3) выражено в табл/ 3 в стоимостных единицах, то очевидно, что суммарный запас ресурсов предприятия составляет 14800 денежных единиц.
На основании исходных данных требуется составить математическую модель для определения плана выпуска продукции.
Решение. Обозначим через х1, x2, х3, х4 - количество выпускаемой продукции видов А, В, С, В, которое необходимо определить.
Теперь составляем ограничения. Из табл. 3 видно, что для выпуска единицы продукции А требуется 6 единиц трудовых ресурсов, B, С, D - соответственно 4, 2, 1 единиц трудовых ресурсов. Тогда необходимый трудовой ресурс для выпуска всех видов продукции будет равен 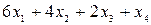 .
.
Очевидно, что потребный ресурс не может превышать располагаемый, т.е. для трудового ресурса будет справедливо неравенство
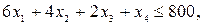
где 800 - располагаемый ресурс (табл. 3).
Если составить аналогичные зависимости для остальных видов ресурсов и добавить предельно допустимые значения выпуска каждого вида продукции, то получим систему:
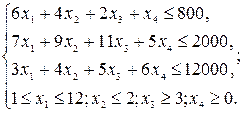
В этой системе неравенства, устанавливающие зависимости для ресурсов, - ограничения, а предельно допустимые значения переменных - граничные условия. В ограничениях левые части неравенства - потребные ресурсы, а правые - располагаемые.
Если в неравенства ввести дополнительные переменные:  , то можно записать
, то можно записать
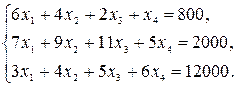
В этой системе уравнений дополнительные переменные означают разность между располагаемым ресурсом и потребным и, следовательно, равны недоиспользуемым величинам ресурсов, т.е. это резервы каждого вида ресурсов.
Очевидно, что система, содержащая 3 уравнения и 7переменных, имеет бесчисленное множество решений, т.е. различных вариантов плана. Все эти возможные варианты, включающие удовлетворяющие системе значения основных и дополнительных переменных, являются допустимыми планами.
Если получить оптимальное решение очень важно, то иметь допустимое решение - необходимо.
Итак, любая, разумеется, правильно составленная (как и в данном примере) задача планирования имеет бесчисленное множество допустимых решений. Какое из них выбрать?
Чтобы ответить на этот вопрос, необходимо сформулировать задачу оптимизации в какой-либо из двух взаимоисключающих постановок.
Обозначим F - ресурсы, R - результат их применения. Тогда при заданных зависимостях результата и потребных ресурсов от количества выпускаемой продукции 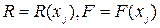 обе постановки распределения ресурсов в сокращенной записи можно представить:
обе постановки распределения ресурсов в сокращенной записи можно представить:
- для первой постановки -
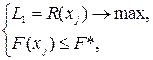
- для второй постановки -
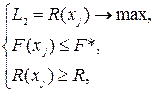
где F*, R* - заданные (плановые или прогнозируемые) величины ресурсов и результата.
Для составления модели в какой-либо постановке потребуются дополнительные данные относительно единичной эффективности производства и реализации каждого вида продукции предприятия, например, прибыль от реализации единицы продукции каждого вида и плановая прибыль в целом от производства всей продукции.
Пусть для продукции видов А, В, С, D она составит соответственно 5, 6, 7 и 8 денежных единиц, а суммарная прибыль от всего производства должна быть не менее 3000 денежных единиц.
Тогда для первой постановки к уже составленной системе ограничений и граничных условий добавляем целевую функцию и получаем математическую модель:

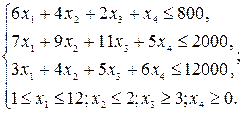
Для второй постановки:
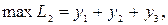
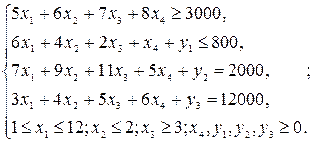
Так как 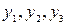 - резервы по ресурсам, то максимизация их суммы обеспечивает минимизацию используемых ресурсов.
- резервы по ресурсам, то максимизация их суммы обеспечивает минимизацию используемых ресурсов.
Из решения задачи в двух различных постановках (см. табл. 4) видно, что результаты решения тоже различные.
Таблица 4
| Поста-новка | Целевая функция | Граничные условия | R0 | F0 | 
| 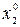
| 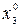
| 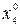
| 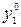
| 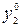
| 
|
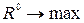
| F ≤14800 | ||||||||||
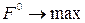
| R ≥3000 | 371,75 | 416,25 | 101,25 | 9751,5 |
В первой постановке max L1 = 3162 денежных единиц. Общее количество использованных ресурсов F = 4774 единиц. При этом ресурсы оказались подразделенными на две группы: лимитирующие, для которых уi = 0, и нелимитирующие, для которых уi > 0. К первой группе относятся: материальные ресурсы, ко второй - трудовые и финансовые. Значит, увеличение запасов материалов позволит найти такой новый оптимальный план производства и реализации продукции, выполнение которого приведет к увеличению прибыли, а прирост трудовых и финансовых, по которым и так имеются резервы в объемах у1 = 396 и у3 = 9630 единиц, - нет.
Отсюда следует, что для повышения эффективности производства (роста прибыли предприятия) потребуется увеличение запасов не всех ресурсов, а только лимитирующих (на практике же, как правило, стремятся к необоснованному наращиванию запасов всех ресурсов по известному принципу «запас карман не тянет»).
Во второй постановке суммарный расход ресурсов оказывается несколько меньше и составляет F = 4531 единиц, и для всех их видов есть резервы.
Таким образом, по результатам после оптимизационного анализа сформулированной нами в обеих постановках задачи распределения ресурсов можно сделать следующие весьма важные для эффективного менеджмента предприятия выводы:
1) реализация найденных оптимальных планов обеспечивает достижение цели предприятия - максимальной эффективности деятельности (или по максимально возможной величине прибыли от реализации, или по минимуму издержек - расхода наиболее важнейших для предприятия ресурсов), особенно если его изделия конкурентоспособны;
2) реализация найденных оптимальных планов будет возможна даже в условиях высвобождения денежных средств, связанных в излишних, сверх требуемых на выполнение этих планов, запасах ресурсов. Понятно, что реализация излишних запасов ресурсов в пределах выявленных резервов будет способствовать еще большему росту эффективности деятельности предприятия, а значит, и стабилизации его рыночных позиций.
Конечно, все эти потенциальные возможности предприятия достигаются, если: а) подобную задачу в любой из этих постановок или в обеих постановках менеджеру удалось сформулировать, для чего необходимо будет предварительно подготовить исходные данные; б) подобную задачу удалось решить, что возможно только при сбалансированности и совместности ее условий.
Поиск по сайту: