АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Условия оптимальности

Читайте также:
  1. A) подписать коллективный договор на согласованных условиях с одновременным составлением протокола разногласий
  2. I Распад аустенита в изотермических условиях
  3. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  4. I. Неблагоприятные условия для жизни бактерий создаются при
  5. I. Правила поведения в условиях вынужденного автономного существования.
  6. I. При каких условиях эта психологическая информация может стать психодиагностической?
  7. I. Психологические условия эффективности боевой подготовки.
  8. II. Условия признания гражданина инвалидом
  9. IV. Дом - Дом, окружающая среда, внешние и внутренние условия, родители
  10. IV. ТРЕБОВАНИЯ К УЧАСТНИКАМ И ИХ УСЛОВИЯ ДОПУСКА
  11. V. Финансовые условия участия в Конкурсе
  12. VI ПРИЧИНЫ, УСЛОВИЯ И ВТОРЖЕНИЕ

 

Предположим, что задача линейного программирования (1) - (3) обладает планами и каждый ее опорный план невырожден. В этом случае для опорного плана (5) имеем 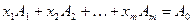(12) (13), где - это значение линейной формы, соответствующее плану . Разложение любого вектора 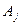по векторам базиса - единственно.

(14)

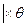
(15)

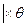
Теорема (для задачи на min): Если для некоторого вектора 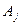выполняются условия , то план 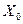не является оптимальным и можно построить такой план X: .

Доказательство:

Умножим равенство (14) на и вычтем из равенства (12), получаем

.

Умножим равенство (15) на и вычтем из равенства (13), получаем

(16).

Следствие: Если для некоторого плана 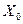разложение всех векторов в данном базисе, удовлетворяющих условию (17), то план 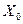является оптимальным. Неравенство (17) это условие оптимальности задачи на минимум, а величины 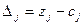- оценки плана.

Теорема (для задачи на max): Если для некоторого вектора 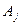выполняются условия , то план 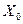не является оптимальным и можно построить такой план X: .

Следствие: Если для некоторого плана 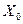разложение всех векторов в данном базисе, удовлетворяющих условию (18), то план 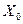является оптимальным. Неравенство (18) это условие оптимальности задачи на минимум, а величины 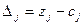- оценки плана.

- формула Жордана-Гаусса.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

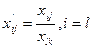
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)