Игры без седловых точек

Рассмотри игру заяц – контролер:

Bj Ai	B 1	B 2	Cij
A 1	1,1	-25	α 1=-25
A 2	-1,1		α 2=-1,1
Cij	β 1=1,1	β 2=0	α = -1,1 β =0

α =max(-25;-1,1)=-1,1

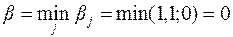
α = -1,1; β = 0

Седловой точки нет.

Рассмотрим игру, заданную платежной матрицей:

Bj Ai	B 1	B 2	Cij
A 1		-1	α 1=-1
A 2			α 2=1
Cij	β 1=3	β 2=5	α =1 β =3

α=max(-1;1)=1=> A ₂.

β = min(3; 5) = 3 => B ₁.

α ≠ β, применение своей максиминной стратегии гарантирует игроку выигрыш: α = 1, а применение своей минимаксной стратегии гарантирует игроку проигрыш: β = 3.

Естественно, что в данной ситуации игрок A хотел бы выиграть больше чем 1, а игрок B проиграть меньше чем 3. например, того и другого одновременно устроило бы значение выигрыша и проигрыша равного соответственно 2.

Так как применение любой чистой стратегии не дает возможность повысить средний выигрыш, то следует использовать более сложную, смешанную стратегию, которая содержит чистые стратегии в качестве элементов. В одноходовой игре, каждый игрок использует только одну стратегию, поэтому, смешанная стратегия имеет смысл при многократном повторении игры.

Каждая стратегия используется в смешанной со своей относительной частотой. Если частота не равна нулю, то стратегия называется активной, ее игрок использует; если частота равна нулю, то фактически этой стратегией игрок не пользуется.

Рассмотрим игру, в которой у игрока A имеется m стратегий A_i, у B – n стратегий B_j с платежной матрицей 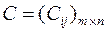, 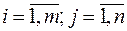. И пусть игра седловой точки не имеет, α ≠ β.

Смешанные стратегии и игроков A и B будем искать в виде:

,

где x_i – это вероятность (частота), с которой игрок A применяет чистую стратегию A_i, а y_j – вероятность (частота), с которой игрок B применяет чистую стратегию B_j.

Средний выигрыш игрока A при этом будет определятся, как математическое ожидание его выигрышей:

– это функция двух наборов и .

Цель игрока A –увеличение своего выигрыша за счет применения своей смешанной стратегии при наилучшей игре игрока B, цель которого уменьшение своего проигрыша. Таким образом, для решения игры надо найти такие и , при которых:

Нижняя цена игры:

Верхняя цена игры:

И оптимальными будут такие стратегии и , при которых

α=β=v, то есть v = = =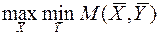

Число v = называется ценой игры.

Основная теорема теории игры, доказанная Нейманом утверждает, что каждая матричная игра с нулевой суммой имеет оптимальные смешанные стратегии.

Теорема Неймана: Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно среди смешанных стратегий.

Пусть ; – пара оптимальный стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Справедлива теорема об активных стратегиях.

Теорема. Если один из игроков придерживается своей оптимальной стратегии, то выигрыш остается неизменным и равным цене игры V, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое значение, так как дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Рассмотрим игру 2×2, – простейший случай конечной игры. Если игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий.

Пусть седловой точки нет, тогда существует пара оптимальных смешанных стратегий: ; . Найдем их, используя теорему об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии , то его средний выигрыш будет равен цене игры V, какой бы активной стратегией не пользовался игрок В. Для игры 2×2 любая читсая стратегия противника является активной, если нет седловой точки.

Выигрыш игрока А (проигрыш игрока В) – случайная величина, математическое ожидание которой и есть цена игры. Поэтому средний выигрыш игрока А будет равен V и для 1-й, и для 2-й чистых стратегий игрока В.

Пусть платежная матрица имеет вид: . Тогда средний выигрыш игрока А, если использует свою смешанную стратегию: , а игрок В свою чистую стратегию В ₁ будет равен цене игры V: ; если игрок В использует стратегию В ₁, то этот выигрыш также равен V, т.е. и . Получаем систему уравнений для определения оптимальной стратегии и цены игры V:

Решив эту систему, получим:

и цена игры:

Применяя теорему об активных стратегиях при нахождении оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (А ₁ или А ₂) средний проигрыш игрока В равен цене игры:

Решив эту систему, получим:

Эти значения и определяют оптимально-смешаную стратегию игрока В.

Пример: Рассмотрим игру «Поиск». Игрок А может спрятаться в одном из убежищ I или II. Игрок В ищет игрока А и если найдет, то получает штраф от игрока А в 1 ден.ед., в противном случае платит игроку А 1 ден.ед. построить платежную матрицу и найти цену игры.

Решение.

У игрока А две стратегии:

А ₁ – спрятаться в убежище I;

А ₂ – спрятаться в убежище II.

У игрока В тоже две стратегии:

В ₁ – искать в убежище I;

В ₂ – искать в убежище II.

Платежная матрица имеет вид:

Bj Ai	B 1	B 2
A 1	– 1		– 1
A 2		– 1	– 1
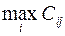
			α=-1 β=1

Найдем решение в смешанных стратегиях:

;

Решив системы, найдем: .

Вывод: каждое из убежищ выбирается с вероятностью .

Поиск по сайту: