II Формула Тейлора с остаточным членом в форме Пеано

Теорема 1. Пусть функция 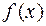имеет в точке 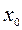производные до п- го порядка включительно. Тогда для остаточного члена имеет место равенство

при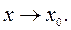

Доказательство. Прежде всего, заметим, что существование производных 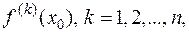означает следующее: функция 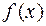имеет производные до 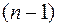-го порядка в некоторой окрестности точки 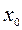, и имеет производную п- го порядка в самой точке .

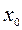Для доказательства теоремы достаточно показать, что

В силу соотношений (2) к этому пределу можно (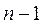) раз применить правило Бернулли–Лопиталя:

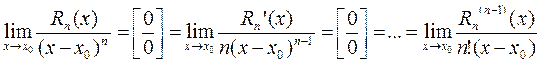
Учитывая все те же соотношения (2), последний предел можно записать как

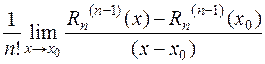
Но этот предел есть не что иное как определение производной функции в точке , т.е. он равен . Но в силу (2) эта производная равна . Итак

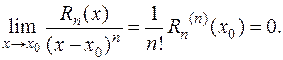
Теорема доказана.

Выпишем формулу Тейлора с учётом доказанной теоремы:

(3)

Замечание 1. Форма Пеано остаточного члена полезна при использовании формулы Тейлора для вычисления пределов.

Замечание 2. Формула (3) является естественным обобщением формулы бесконечно малых приращений (тема «Производная», §4), которую можно записать так: она получается из (3) при п = 1.

Поиск по сайту: