Баланс финансово-кредитной операции

Необходимым условием финансовой или кредитной операции в любом ее виде (ссуда, депозит, заем, инвестиции в проект и т.д.) является сбалансированность вложений и отдачи. На этом требовании базируются все рассмотренные в двух предыдущих главах методы планирования погашения задолженности. Посмотрим теперь на проблему сбалансированности с более общей, теоретической точки зрения, не отвлекаясь на технические детали расчета сумм обслуживания долга и ее компонент.

Для этого вернемся к графику, который был назван в гл. 1 контуром операции. Напомним, что контур позволяет составить уравнение, балансирующее вложение средств и отдачу от них. Для случая, показанного на рис. 9.1, получим следующие размеры задолженности после уплаты R ₁ и R ₂:

где q^t = (1 + i) ^t — множитель наращения, i — ставка процентов по кредиту.

Очевидно, что баланс кредита и погасительных платежей имеет место в том случае, когда последний платеж замыкает контур. В нашем примере полная сбалансированность означает

Определим K ₂через K ₀и подставим полученный результат в балансовое уравнение:

Балансовое уравнение становится весьма громоздким, если число временных интервалов больше трех. Поэтому преобразуем найденное выражение, после чего

(9.1)

где

Найденное балансовое уравнение для нас ценно прежде всего в методологическом плане. Здесь ясно показано, что кредитная операция при применении сложных процентов может быть расчленена без какой-либо потери точности на два как бы встречных процесса: наращение первоначальной задолженности за весь период и наращение погасительных платежей за срок от момента платежа и до конца срока операции. Назовем такой подход методом "встречных операций". В ряде случаев он существенно упрощает доказательства, и в дальнейшем мы неоднократно будем его применять.

Умножив (9.1) на дисконтный множитель v^T, получим

Иначе говоря, сумма современных величин погасительных платежей на момент выдачи кредита равна при полной сбалансированности платежей сумме этого кредита. Это положение уже применялось нами, правда, на интуитивном уровне, при планировании погашения задолженности.

Обобщим (9.1) для случая с n погасительными платежами

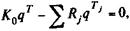j = l, 2,..., n,

где Т_j — время от момента платежа R_j до конца срока.

При написании балансового уравнения предполагалось, что процентная ставка постоянна на всем протяжении операции. Принципиально ничего не меняется, если значение ставки изменяется во времени. Допустим, что изменение происходит на каждом шаге. Тогда можно записать

где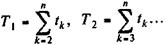

Балансовые уравнения, о которых только что шла речь, позволяют решить несколько важных в практическом отношении задач, а

именно: измерить доходность от операции и распределить получаемый доход по их источникам и периодам, предусматриваемым условиями контракта, или по календарным отрезкам времени. Для этого, однако, надо разработать балансовые уравнения, в которых наращение (или дисконтирование) производится по неизвестной ставке, характеризующей полную доходность. Именно таким путем определяются эти величины в следующих параграфах.

Поиск по сайту: