Энтропия идеальных газов

Для получения рассчетного выражения изменения энтропии идеальных газов воспользуемся первым законом термодинамики, в котором теплота определяется с использованием изменения энтальпии

(4.58)

Для идеального газа изменение энтальпии определяется как dh=c_PdT, а удельный объем v=RT/P. Подставив данные выражения изменения энталпии и удельного объема в уравнение (4.58), получим уравнение для изменения энтропии идеального газа

(4.59)

Разность энтропий идеального газа в конкретных двух состояниях можно получить интегрированием выражения (4.59)

(4.60)

Воспользовавшись формулой Майера с_Р=с_V+R и уравнением Менделеева-Клапейрона Pv=RT, выражение (4.60) можно записать и через две другие пары термических параметров состояния

(4.61)

Для определения абсолюного значения энтропии идеального газа необходимо зафиксировать начало ее отсчета любой парой термических параметров состояния. Например, приняв s₀=0 при Т₀ и Р₀, воспользовавшись уравнением (4.60), получим

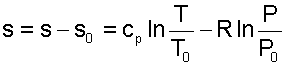
(4.62)

Выражение (4.62) свидетельствует о том, что энтропия идеального газа есть параметр состояния, поскольку ее можно определить через любую пару параметров состояния. В свою очередь, поскольку энтропия сама является параметром состояния, используя ее в паре с любым независимым параметром состояния, можно определить любой другой параметр состояния газа.

Поиск по сайту: