Энергия заряженного проводника. Энергия конденсатора

Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна

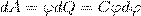");?>" alt="элементарная работа сил электрического поля заряженного проводника">

Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу

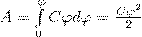(2)

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

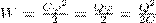(3)

Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем

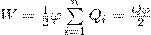
где Q=∑Q_i - заряд проводника.

3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна

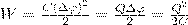(4)

где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.

Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда

(5)

Подставив в (4) выражение для емкости плоского конденсатора, получим

(6)

Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:

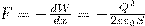
где знак минус указывает, что сила F является силой притяжения.

Поиск по сайту: