 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Статистичний розподіл вибірки та його геометричне зображення
Нехай вивчається деяка випадкова величина Х, закон розподілу якої невідомий. З цією метою над випадковою величиною Х проводиться ряд незалежних випробувань (вимірів). Результати вимірювань заносять в таблицю, що називають статистичним рядом, яка є первинною формою опису статистичного матеріалу і може бути оброблена різними способами, наприклад:
а) статистичним розподілом вибірки називається таблиця, в якій вказані значення х ознаки Х у зростаючому порядку (в цьому випадку значення утворюють дискретний варіаційний ряд, самі значення ознаки називаються варіантами), а також відповідні частоти або відносні частоти
| Варіанти Х | Х1 | Х2 | … | Хі | … | Хk |
| Частота ni | n1 | n2 | … | ni | … | nk |
Відносна частота 
| 
| 
| … |
| … | 
|
де n=n1+n2+…nk,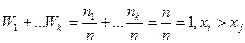 
, якщо i>j, 
;
б) якщо згрупувати значення ознаки в зростаючому порядку в інтервалі довжиною h (крок інтервалу), то одержимо інтервальний варіаційний ряд. Вказавши число ni значень ознаки, що попали в і -ий інтервал, і звівши дані в таблицю, одержимо статистичний розподіл інтервального варіаційного ряду
| Варіант-інтервал h=xi-xi-1 | [x0,x1] | [x1,x2] | … | [xi-1,xk] | … | [xk-1,xk] |
| Частота ni | n1 | n2 | … | ni | … | nk |
| Відносна частота Wi | W1 | W2 | … | Wi | … | Wk |
де весь інтервал значень 
.
в) статистичною (емпіричною) функцією розподілу вибірки називається закон зміни частоти події X<x в даному статистичному матеріалі:
, (1)
де n(x) – число значень варіант, для яких 
, n – об’єм вибірки; тобто щоб знайти, наприклад, F*(x3), потрібно число варіант, менших х3, розділити на весь об’єм вибірки n.
Аналогом теоретичної диференціальної функції (густини) розподілу служить щільність відносної частоти
. (2)
На відміну від емпіричної функції розподілу вибірки функція розподілу F(x) генеральної сукупності називається теоретичною функцією розподілу. Різниця між ними полягає в тому, що теоретична функція F(x) визначає ймовірність події X<x, а емпірична функція F*(x) визначає відносну частоту цієї ж події. По теоремі Бернуллі при 
по ймовірності. Іншими словами, при великих n числа F*(x) і F(x) мало різняться одне від одного в розумінні, що 
. Звідси можна зробити висновок про доцільність використання емпіричної функції розподілу вибірки для наближеного представлення теоретичної (інтегральної) функції розподілу генеральної сукупності.
Такий висновок підтверджується ще й тим, що F*(x) має всі властивості F(x). Дійсно, з означення функції F*(x) випливають її властивості:
1) 
2) F*(x) - неспадна функція;
3) якщо х1 – найменша варіанта, то F*(x)=0 при x<x1, якщо xk – найбільша варіанта, то
F*(x)=1 при x>xk.
Отже, емпірична (статистична) функція розподілу вибірки є оцінкою теоретичної функції розподілу генеральної сукупності.
Для наочного зображення статистичних розподілів використовують графіки та діаграми: полігон, гістограму, кумуляту, огіву.
Полігон частот – многокутник (ламана), побудований в системі координат (x,ni) або (x,Wi) (полігон частот або відносних ачастот). Для його побудови на осі абсцис відкладають варіанти хі, а на осі ординат – відповідні їм ni чи Wi. Точки (xi,ni) чи (xi,Wi) з’єднують відрізками прямих і отримують полігон частот.
Гістограма – діаграма в системі координат 
. Її доцільно будувати у випадку неперервної ознаки, для чого інтервал, в якому містяться всі спостережувані значення ознаки розбивають на декілька часткових інтервалів довжиною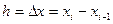 
і знаходять для кожного часткового інтервалу ni – суму частот ваірант, що попали в і -ий інтервал. Для її графіка будується ступінчата фігура, що складається з прямокутників, основами яких є частинні інтервали довжиною h, а висоти рівні відношенню 
або 
. Отже, на осі абсцис відкладаються частинні інтервали, а над ними проводять відрізки, паралельні осі абсцис на висоті 
. Тоді площа і -го частинного прямокутника рівна 
- сумі частот варіант (відносних частот) і -го інтервалу, а площа гістограми частот рівна об’єму вибірки 
чи 
.
Кумулята – ламана лінія в системі координат (x,F*(x)) (для дискретного варіаційного ряду).
Огіва – крива в системі координат (x,F*(x)) (для інтервального ряду).
Приклад 1. Скласти таблицю статистичного розподілу розміру Х чоловічого взуття, яке продане магазином протягом дня: 39, 40, 41,40, 43, 41, 44, 42,40,42, 41, 41, 43, 42, 39, 42, 43, 41, 42, 41, 38, 42, 42, 41, 40, 41, 43, 39, 40, та побудувати полігон та кумуляту.
Рішення. Таблиця розподілу дискретного ряду має вигляд:
| № п/п | Варіанта Х- розмір взуття | Частота ni | Частота Ni | n(x) | F*(x) |
| 1 | 38 | 1 | 1/30 | 1 | 1/30 |
| 2 | 39 | 3 | 1/10 | 4 | 2/15 |
| 3 | 40 | 5 | 1/6 | 9 | 3/10 |
| 4 | 41 | 9 | 3/10 | 18 | 3/5 |
| 5 | 42 | 7 | 7/30 | 25 | 5/6 |
| 6 | 43 | 4 | 2/15 | 29 | 29/30 |
| 7 | 44 | 1 | 1/30 | 30 | 1 |
Приклад 2. Побудувати гістограму відносних частот розподілу в першому стовпці вказано частинні інтервали, в другому – сума частот варіант частинного інтервалу:
2 – 5 9
5 – 8 10
8 – 11 25
11 – 14 6
| Частинні інтервали з кроком h=3 | Сума відносних частот варіант інтервалу Wi | Густина частоти |
| 2-5 | 9/50 | 3/50 |
| 5-8 | 10/50 | 1/15 |
| 8-11 | 25/50 | 1/6 |
| 11-14 | 6/50 | 1/25 |
Рішення. Складемо таблицю, де n=9+10+25+6=50, 
.
Поиск по сайту: