Рівняння руху Коші

Для рівноваги довільно виділеного об’єму пружного середовища під дією систем поверхневих і об’ємних сил, включаючи сили інерції, вимагається, щоб результуючі сили і момент, діючих на цей об’єм, дорівнювали нулю.

Виділимо в пружному тілі елемент об’єму . Компоненти сил інерції, діючих на елементарний об’єм , будуть:

; ; , (2.4)

де: - густина тіла; - компоненти переміщення; - час.

Проекції прискорення в (2.4) можна визначити з формул (1.5), диференціюючи які, отримаємо

Для об’єму пружного тіла компоненти сил інерції будуть:

. (2.5)

В якості зовнішніх сил, діючих на об’єм (рисунок 2.1), маємо об’ємні сили, наприклад, силу тяжіння, з компонентами , і сили пружних напружень, прикладених до поверхні об’єму V, з компонентами , , .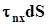

Для об’єму V пружного тіла компоненти сили тяжіння будуть:

; ; . (2.6)

Компоненти сил пружних напружень, прикладених до поверхні об’єму V

; ; . (2.7)

Враховуючи (2.5), (2.6) і (2.7), запишемо умову рівноваги довільного об’єму V пружного середовища під дією проекцій сил на вісь :

. (2.8)

Підставимо в (2.8) значення з (2.2) і за допомогою теореми Гауса-Остроградського перейдемо від інтегралу по поверхні до інтегралу по об’єму:

. (2.9)

В силу довільності об’єму V:

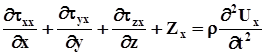. (2.10)

Аналогічно, співставляючи умови рівноваги довільного об’єму пружного середовища під дією компонент сили на осі і , отримаємо

, (2.11)

. (2.12)

Вирази (2.10) і (2.12) – рівняння руху деформованого тіла.

Якщо пружне тіло знаходиться в рівновазі під дією заданих сил, то компоненти сил інерції дорівнюють нулю, і рівняння рівноваги набувають вигляду:

(2.13)

Для рівноваги довільного об’єму V пружного середовища крім того необхідно, щоб результуючий момент сил, діючих на цей об’єм, дорівнював нулю.

Наприклад, умова рівноваги моментів сил, діючих на елементарний об’єм, відносно осі, паралельній х (рис.2.3), необхідно виконання рівності

,

звідки

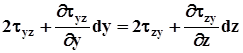
При 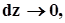отримаємо співвідношення

.

Аналогічні вирази можна отримати для моментів сил відносно вісей у та z:

Таким чином, в загальному випадку справедливе співвідношення

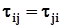, (2.14)

яке показує, що тензор напружень є симетричним.

Якщо врахувати рівність (2.14), напружений стан в будь-якій точці деформованого тіла визначається шістьма компонентами напруження: , , , , , .

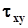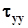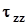Рівняння (2.10-2.14) вперше були отримані Коші. Вони відіграють важливу роль у теорії пружності.

Рисунок 2.3. - До рівняння рівноваги моментів сил, діючих на гранях елементарного об’єму.

Поиск по сайту: