АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Рівняння Ламе

Читайте также:
  1. Бюджетні обмеження споживача, бюджетне рівняння та фактори впливу на бюджетну лінію.
  2. Геометричний зміст похідної. Рівняння дотичної.
  3. Грошовий обіг та його закони. Рівняння грошової та товарної мас (рівняння Ірвена Фішера). Грошові агрегати.
  4. Загальне рівняння фотосинтезу та походження кисню
  5. Змістовний модуль 6.2. «Рівняння, їх системи і сукупності.».
  6. Знаходження параметів лінійного рівняння регресії методом найменших квадратів
  7. КОМПЛЕКСНІ ХВИЛЬОВІ РІВНЯННЯ
  8. Лінійна кореляція і рівняння лінійної регресії
  9. Малюнок № 6.1. Графік рівняння кола.
  10. Моделі состава, відчепу і вагона. Диференціальне рівняння скочування відчепів з гірки
  11. Найбільш просте рівняння стану системи – рівняння стану для 1 моль ідеального газу
  12. Оцінка тісноти та значимості зв’язку між змінними у рівняннях парної регресії

Випишемо диференціальне рівняння руху пружнього середовища (2.10), (2.11) і (2.12):

(4.1)

Перетворимо ці рівняння, виразивши в них напруження через переміщення. Для цього скористаємося узагальненим законом Гука в переміщеннях (3.20). Вибираючи в (3.20) напруження, що входять в перше з рівнянь (4.1), і диференціюючи їх, отримаємо

(4.2)

Вносячи (4.2) в перше рівняння (4.1), отримаємо

 

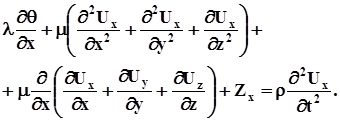
Враховуючи

будемо мати

Аналогічно можна перетворити і два інших рівняння (4.1). В результаті перетворень система рівнянь (4.1) набуде вигляду

(4.3)

Ці рівняння теорії пружності в переміщеннях вперше отримав Ламе. Рівняння (4.3) узагальнюють висновки, що були зроблені раніше. Якщо сили інерції дорівнюють нулю, то отримаємо рівняння рівноваги елементарного об’єму (рівняння Коші); якщо сили інерції не дорівнюють нулю, то маємо рівняння руху елементарного об’єму при деформаціях. Одночасно ці рівняння показують зв’язок між напруженнями та деформаціями для ізотропних тіл через коефіцієнти Ламе.

Три рівняння(4.3) можна перетворити в одно векторне:

(4.4)

оскільки

.

У математичному відношенні зміст теорії розповсюдження сейсмічних хвиль пов’язано з рішенням рівняння (4.3) при виконанні початкових та граничних умов. Початкові умови – це умови на початку руху. На початку руху при t =0, необхідно задати значення переміщень Ux, Uy, Uz та їх похідні по часу t. Зазвичай припускається, що початкові умови, які відносяться до моменту включення дії, рахуються нульовими. Граничні умови – це умови на граничних поверхнях: на вільній границі (денній поверхні), на границі розділу двох пружних середовищ. На вільній границі може бути задано значення зовнішньої сили, прикладеної до деякого елемента цієї границі. Умови на границі розділу середовищ рахуються такими, що при переході через цю границю залишаються неперервними значення векторів зміщення і напружень. Такий контакт двох середовищ називається жорстким.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)