Хвильові рівняння в перших похідних

У роботі О.К.Кондратьєва^* введено поняття оптимального хвильового рівняння (ОХР). Це рівняння, яке описує лінійно-непружне середовище, не містить похідних по часу вище другого порядку, і добре узгоджується у сейсмічному діапазоні частот з експериментальними залежностями фазової швидкості 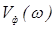та коефіцієнта поглинання пружних хвиль 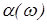від частоти.

^*Кондратьев О.К. Отраженные волны в поглощающих

средах. М.: “Недра”, 1983г. - 231 с.

ОХР по числу параметрів (три) реологічної моделі середовища узгоджено з числом параметрів спостереженого хвильового поля, які надійно можна визначити експериментально.

Разом з цим, при виводі ОХР О.К.Кондратьєвим накладається не зовсім обґрунтоване, на наш погляд, обмеження на число коренів для комплексного числа К. Виходячи з поширення двох однакових хвиль з рівною швидкістю, але в різних напрямках при збудженні коливань у внутрішній точці середовища, він приходить до висновку, що ОХР повинно містити гуківське хвильове співвідношення (6.2)

Інакше кажучи, члени ОХР з парними похідними визначають наявність хвильового процесу, а з непарними похідними поля зміщення - дисипацію пружної енергії.

В сейсморозвідці найбільш поширено збудження хвиль на границі пружного півпростору - земної поверхні або у безпосередній близькості до неї. У всякому випадку, сейсморозвідників цікавить хвиля, яка поширюється вниз, тобто хвиля, яка зондує геологічне середовище. Тому нас влаштовують і такі хвильові рівняння, які дають один корінь для хвильового числа К, тобто описують лише одну хвилю, яка поширюється вниз (в одну сторону від джерела). На можливість використання для аналізу хвильових процесів диференційних рівнянь першого порядку, які дають одне значення К, вказано у роботах Дж. Уізема, який за основу

приймає не хвильове рівняння (6.2), а більш просте

. (6.22)

Тепер, коли хвильовий процес описується першими похідними зміщення, для того, щоб К було комплексним, тобто, щоб 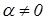, у рівняння (6.22) необхідно добавити дисипативний член у вигляді парної похідної . Таким чином, будемо розглядати хвильове рівняння виду

. (6.23)

Для того, щоб включити в клас (6.23) хвильове рівняння з дисипативним членом, пропорційним зміщенню часток середовища, припустимо .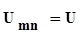

Основні властивості рівняння (6.23) приведені в таблицях 6.1 та 6.2.

З таблиць видно, що експериментальним даним про фазові швидкості найбільш відповідають моделі 1 та 4, для моделі 2 характерна пропорційність швидкості , для третьої - пропорційність .

Зупинимось більш детально на аналізі 1 та 4 моделей.

Перейдемо від рівняння

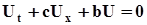(6.24)

до рівняння стану середовища, враховуючи, що , де - градієнт напруження, - щільність середовища, а деформація

(6.25)

Щоб перейти від рівняння стану до рівняння, яке зв’язує напруження та деформацію у явному вигляді, проінтегруємо (6.25) по X і продиференціюємо по t. Беручи до уваги, що

при с =const, а профіль хвилі розгорнутий на 180 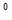у порівнянні з її графіком, отримаємо

(6.26)

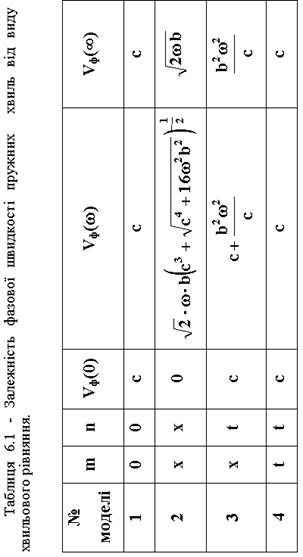
або

, (6.26’)

де - модуль пружності, .

При з (6.26) отримаємо

,

тобто залишкова деформація пропорційна коефіцієнту поглинання, швидкості поширення пружної хвилі та інтегралу попередніх деформацій.

Недоліком першої моделі є постійність коефіцієнта поглинання по всьому діапазоні частот при постійному коефіцієнті b, що не узгоджується з експериментальними даними.

Поиск по сайту: