Профілях

Серед методів ХZ - сейсморозвідки, запропонованої нами, одне з чільних місць посідає процедура коректної міграції хвильового поля, тобто продовження хвильового поля без необхідності попереднього завдання розподілу швидкості. Більш того, цей розподіл швидкості поширення пружних хвиль буде визначений в процесі міграції хвильового поля U(х,z,t), січення якого U(х,0,t) та U(0,z,t), були зареєстровані на співпряжених горизонтальному та вертикальному профілях на польовому етапі ХZ-сейсморозвідки. Домовимося, що крок спостереження на вертикальному та горизонтальному профілях однаковий і значно менше довжини хвилі

,

а крок квантування сейсмічного запису , де V_m - максимальна очікувана швидкість поширення хвиль. Ці умови дозволяють нам в подальшому перейти від часткових похідних до кінцевих різниць при побудові обчислювальної схеми коректної міграції часового поля.

Міграцію будемо проводити на підставі хвильового рівняння в часткових похідних першого порядку (9.2), але більш складну в обчислювальному аспекті процедуру, можна побудувати і на основі звичайного хвильового рівняння

Розглянемо елементарний міграційний куб 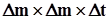,в якому позначимо вершини наступним чином:

Поле в шостій вершині будемо шукати за його значенням в п'яти попередніх. Для цього піднесемо до квадрату рівняння (9.2).

Рівняння (9.5) (до речі, зверніть увагу на його подібність до рівняння ейконалу) запишемо двічі через кінцеві різниці

(9.9)

(9.10)

Поиск по сайту: