 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Центр ваги твердого тіла
Центром ваги тіла називають центр системи паралельних сил, яку наближено утворюють сили ваги його елементарних частинок.
Радіус-вектор центра ваги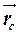 
підраховують як радіус-вектор центра паралельних сил (рис.1.9) за формулою:
 ,
|
де: 
- радіус-вектор точки прикладання сили ваги елементарної частинки 
;
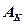- вага елементарної частинки;
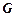- вага всього тіла.
В граничному випадку, коли число елементарних частинок n прямує до нескінченості, формула (1.35) набуває вигляду:
 .
|
У свою чергу 
і тому:
 ,
|
де: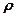 
- густина речовини тіла; 
- елементарний об’єм частинки тіла;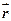 
- радіус-векор елементарної частинки.
Рисунок 1.9 – Радіус-вектор центра паралельних сил
Координати центра ваги тіла визначаються рівняннями:
 ,  ,  .
|
Якщо тіло є однорідним, то 
і 
. В такому випадку
 ,  ,  ,
|
де, 
- об’єм тіла.
Узагальнення результатів визначення центрів ваги однорідних тіл приводить до висновку: якщо однорідне тіло має площину, вісь або центр симетрії, то центр його ваги розташований відповідно або в площині симетрії, або на осі симетрії, або в центрі симетрії.
Методика визначення центра ваги тіл полягає в наступному. Тіло розбивають на скінчену кількість таких частин, для кожної з котрих положення центра ваги відоме, або може бути попередньо визначено. Далі центр ваги підраховують за загальними формулами. Так, наприклад, координати центра ваги плоскої однорідної фігури визначаються з рівнянь:
 ;  ,
|
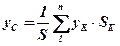у котрих 
- кількість простих фігур (коло, прямокутник, трикутник), на які розбита задана фігура;
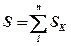- площа всієї фігури;
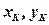- координати центра ваги 
-ї простої фігури площею 
.
Питання для самоконтролю
1. Якими параметрами визначається сила, що діє на тверде тіло?
2. Що таке лінія дії сили?
3. Що називають проекцією сили на координатну вісь?
4. Які системи сил називають еквівалентними?
5. Яку силу називають рівнодіючою системи сил?
6. Чи може рівнодіюча двох сил бути за модулем менше, ніж модуль складових її сил?
7. Дайте визначення векторного моменту сили відносно довільного просторового центра і наведіть відповідну формулу.
8. Що таке центр ваги тіла? Чи змінюється положення центра ваги відносно точок тіла при переміщенні тіла в просторі?
Поиск по сайту: