Функція витрат та рівновага виробника

Економічні витрати залежать від кількості використаних ресурсів (їх затрат) та цін за послуги факторів виробництва. Тоді можна встановити залежність між обсягами виробництва та мінімально можливими витратами, необхідними для його отримання. Ця залежність називається функцією витрат:

Q = f (PL, L, PK, K), (6.1)

де L, K – затрати праці та капіталу; PL, PK - ціни відповідних ресурсів.

За допомогою функції витрат можна вирішувати як прямі, так і зворотні задачі: мінімізація витрат на заданий обсяг виробництва або максимізація виробництва при заданих витратах.

Легко помітити зв’язок функції витрат з виробничою функцією: яка доповнюється урахуванням цін на відповідні виробничі ресурси.

Загальні (сукупні) витрати (ТС) на виробництво можна розрахувати як суму витрат на придбання кожного фактору:

ТС = PL L + PK K. (6.2)

При фіксованих цінах на ресурси можна знайти різні набори капіталу та праці, які можна придбати за однакові витрати. Графічне зображення цих наборів називається ізокостою. Ізокоста – це лінія, яка відображає затрати капіталу та праці, при яких витрати виробництва залишаються незмінними (рис.6.1).

К

ТС₁ ТС₂ ТС₃ L

Рис.6.1. Ізокости

Кожен рівень затрат праці та капіталу має свою ізокосту. Нахил будь-якої ізокости з сімейства ізокост дорівнює (-DК/DL). Його можна виразити і через співвідношення цін:

–DК/DL= PL/ PK. (6.3)

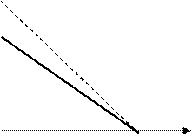
Зміна ціни на працю чи капітал може змінити нахил ізокости (рис. 6.2): зростання ціни капіталу та зниження ціни праці збільшує кут нахилу; кут нахилу відбувається при зростанні ціни праці та зниженні ціни капіталу.

К К

L L

а б

Рис.6.2. Зміна нахилу ізокости під впливом: а – зростання ціни праці;

б – зниження ціни капіталу

Який же із запропонованих ізокостою набір капіталу та праці забезпечить максимальний обсяг продукту? Для відповісти на це запитання потрібно сумістити ізокости з картою ізоквант (рис.6.3).

К

ТС

A

Q₃

Q₂

Q₁

L

Рис.6.3. Максимізація обсягів виробництва при заданих витратах

Умовою для визначення максимальних обсягів виробництва при заданих витратах (як мінімальних витрат на заданий обсяг виробництва) є однаковий нахил ізокости та відповідної ізокванти, що має спільну точку з ізокостою та найбільш віддалена від початку координат (точка А на рис.6.3).

Нахил ізокванти визначається граничною нормою технологічного заміщення, а ізокости – співвідношенням цін праці та капіталу. Тоді умову рівноваги виробника, тобто такого його стану, в якому він не бажає змінювати співвідношення капіталу та праці, що задіяні у виробничому процесі, можна подати як рівність:

MRTSLK = PL / PK. (6.4)

Оскільки MRTSLK = MPL / MPK, то справедливим буде рівняння:

MPL / MPK= PL / PK, (6.5)

або

MPL / PL= MPK / PK. (6.6)

Рівняння 6.6 відображає принцип найменших витрат, суть якого в тому, що виробництво заданого обсягу продукції з мінімальними витратами вимагає, щоб ресурси, які одночасно використовуються, мали однакову величину граничного продукту на одиницю вартості ресурсу. Якщо граничний продукт на одиницю витрат одного фактора перевищує граничний продукт іншого фактора, то фірма може отримати приріст продукції для реалізації без додаткових коштів за рахунок зміни співвідношення факторів виробництва.

Якщо з’єднати точки, що відповідають комбінаціям факторів виробництва, які мінімізують витрати при різних заданих обсягах виробництва, то дістанемо так звану траєкторію зростання (рис.6.4).

К

ТС₃

ТС₂

ТС₁ Q₃

Q₂

Q₁

L

Рис. 6.4. Траєкторія зростання

Траєкторія зростання показує, як змінюється співвідношення факторів виробництва, що забезпечують мінімальні витрати, при збільшенні обсягів виробництва.

Поиск по сайту: