Малюнок № 13.11

Відповідно до ТМО вивчення цієї теми, які вчитель повинен знати, щоб успішно справлятися з викладанням, можна виділити ті ж етапи, що і в роботі над частинами величини. На першому з них проводиться підготовча робота до сприймання нового матеріалу, на другому – первинне усвідомлення поняття дробу, на третьому – формування уявлень про дріб і формування відповідних знань, умінь і навичок.

Вивчення дробів ґрунтується на конкретних образах частин величини та практичному їх утворенні, а потім і дробів у результаті поділу предметів або геометричних фігур на потрібну чи вказану кількість рівних частин. Яка ж основна дидактична мета підготовчої роботи до ознайомлення учнів з дробами? – актуалізація опорних знань, умінь і навичок про частини, а саме: їх утворення, позначення, порівняння, знаходження частини числа та числа за відомою його частиною.

Рекомендується в темі „Дроби” до 50% часу витрачати на удосконалення нових прийомів обчислень і на розв’язування рівнянь та задач. Як же відбувається ознайомлення з дробами? – за допомогою їх утворення з допомогою моделювання на наочних посібниках або при розгляді малюнків підручника. Першим кроком у формуванні початкових уявлень про дроби є нагромадження уявлень про поділ фігур на рівні частини. Поняття дробу вводиться у процесі бесіди вчителя, яка підкріплюється практичними роботами. Вчитель пропонує дітям намалювати смужку та поділити її на 4 рівні частини. Потім дає завдання зафарбувати 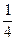її частину. Після цього пропонує відповісти на наступні запитання: скільки частин залишилося не зафарбованими? – три. Яку частину складає не зафарбована частина смужки від усієї? – три четвертих частини. Як би Ви її назвали та записали? Якщо діти не справляться з цим завданням, то вчитель повідомляє: записати це можна так . Такий запис називається дробом. Число 3, яке стоїть над рискою дробу, називається чисельник, а число 4, що стоїть під рискою дробу, називається знаменник. Чи знаєте Ви, що показує знаменник дробу? – на скільки рівних частин поділено величину. А що ж показує чисельник дробу? – скільки таких рівних частин взято. Аналогічна робота проводиться з іншими геометричними фігурами.

Після введення поняття дробу розпочинається систематична робота з формування уявлень школярів про дроби. З цією метою нині діючими підручниками та методичними посібниками для вчителів пропонується певна система вправ. Оскільки вона містить аналогічні вправи, що розглядалися в темі “Частини величин”, то пропонуємо студентам виконати завдання № 31 для самостійної роботи.

Для порівняння дробів використовується роздатковий матеріал (смужки, набір однакових геометричних фігур) та ілюстрації підручника чи таблиць, на яких зображено кілька однакових прямокутників, поділених на різну кількість однакових частин. Для формування вказаних умінь використовується така система вправ: 1) користуючись малюнком, постав замість квадратів такі числа, щоб рівності були правильними, наприклад: /8= 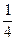; 2) користуючись малюнком, порівняй дроби: , , , , 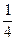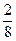і 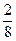; 3) накресліть прямокутник довжиною 16см і шириною 1 см. Під ним накресліть такий же та поділіть його на дві рівні частини. Які частини одержали? Скільки других частин в цілому прямокутнику? Накресліть ще один і поділіть його на чотири рівних частини. Як називається кожна частина? Скільки таких частин? Скільки четвертих частин в половині? 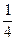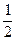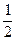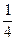Що більше чи ; чи ? 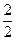чи ? чи ? (див. таблицю № 13.11.). Аналогічно проводиться порівняння інших дробів. 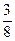4) замість зірочок вставте пропущений знак >, < чи =: * , *1; 5) підставте число у віконце так, щоб нерівність була правильною, наприклад: 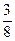>□/4. Зауважимо, що для порівняння беруться дроби із знаменниками, кожний з яких можна одержати з іншого шляхом множення на якесь число чи ділення його на рівні частини.

Поиск по сайту: