 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Правила обчислення похідних
Похідна суми дорівнює сумі похідних  .
.
Доведення:
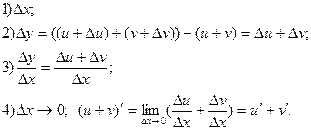
Наслідки:
-похідна різниці функцій дорівнює різниці похідних;
-похідна суми декількох функцій дорівнює сумі похідних цих функцій.
Наприклад: Знайти похідні функцій
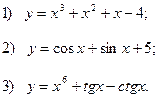
Відповідь: 
Похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну іншої 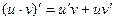 .
.
Доведення:
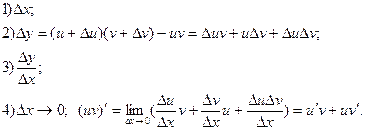
Наслідки:
-сталий множник виноситься за знак похідної;
-похідна добутку декількох множників дорівнює сумі добутків похідної кожного з них на всі останні.
Наприклад: Знайти похідні функцій
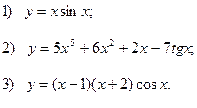
Відповідь: 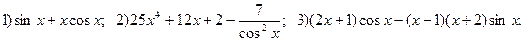
Похідна частки функцій 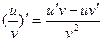 .
.
Доведення:
Скористаємось теоремою про похідну добутку двох функцій
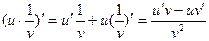 .
.
Наприклад: Знайти похідні функцій
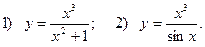
Відповідь: 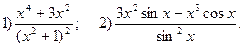
Лекція 27.
Тема: Похідна складеної функції. Похідні показникових, логарифмічних функцій.
План.
1. Поняття складеної функції.
2. Похідна складеної функції.
3.Похідна показникової та логарифмічної функцій.
1. Поняття складеної функції.
Якщо функція g ставить у відповідність числу х число u, а функція f – числу u число у, то кажуть функція у є складеною із функцій g і f, пишуть 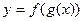 .
.
Функцію g називають внутрішньою, f- зовнішньою функцією. Щоб обчислити значення складеної функції 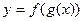 в довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f.
в довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f.
Наприклад: функція 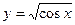 -складена,
-складена, 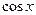 - внутрішня,
- внутрішня, 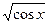 - зовнішня.
- зовнішня.
2. Похідна складеної функції.
У складеній функції 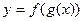 присутня проміжна змінна
присутня проміжна змінна 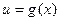 . Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні позначення:
. Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні позначення:
похідна у по х 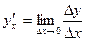 ;
;
похідна у по u 
похідна u по х 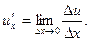
Теорема: Похідна складеної функції 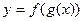 знаходиться за формулою
знаходиться за формулою
 , де
, де 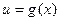 , або похідна складеної функції дорівнює похідній зовнішньої функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.
, або похідна складеної функції дорівнює похідній зовнішньої функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.
Доведення:
Будемо вважати, що функція u має похідну в точці х, а функція f має похідну в точці u, тобто існують границі 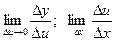 і
і  .
.
Нехай аргументу х надано приросту 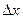 , тоді змінна u набуде приросту
, тоді змінна u набуде приросту 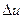 . Функція у також одержить приріст
. Функція у також одержить приріст 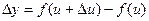 .
.
Подамо 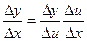 . Якщо
. Якщо 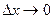 , то
, то 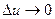 .
.
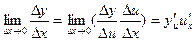 .
.
Наприклад: Знайти похідну функції 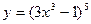 .
.
Розв’язання:
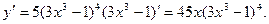
3.Похідна показникової та логарифмічної функцій.
а) Похідна функції 
б) Знайдемо похідну функції 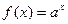 , скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:
, скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції: 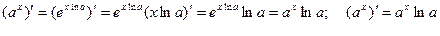 . Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.
. Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.
Наприклад: Знайти похідну функції  .
.
Розв’язання:
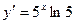 .
.
в) Розглянемо функцію 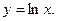 За основною логарифмічною тотожністю
За основною логарифмічною тотожністю  . Диференціюючи обидві частини цієї рівності, одержимо
. Диференціюючи обидві частини цієї рівності, одержимо
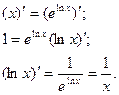
Знайдемо похідну функції  .
.
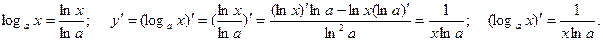
Наприклад: Знайти похідні функцій 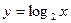 .
.
Розв’язання:
Лекція 28.
Тема: Зростання і спадання функцій. Стаціонарні, критичні точки.
План.
1.Зростання і спадання функцій.
2.Точки екстремуму. Стаціонарні, критичні точки.
1.Зростання та спадання функцій.
Теорема. 1) Якщо функція f(x) має похідну на відрізку [а, b] і зростає на цьому відрізку, то її похідна на цьому відрізку невід’ємна, тобто f¢(x) ³ 0.
2) Якщо функція f(x) безперервна на відрізку [а, b] і диференційована на проміжку (а, b), причому f¢(x) > 0 для а < x < b, то ця функція зростає на відрізку [а, b].
Доведення.
1) Якщо функція f(x) зростає, то f(x + Dx) > f(x) при Dx>0 і f(x + Dx) < f(x) при Dх<0, тоді: 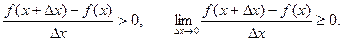
2) Хай f¢(x)>0 для будь-яких точок х1 і х2, що належать відрізку [а, b], причому x1<x2.
Тоді по теоремі Лагранжа: f(x2) – f(x1)= f¢(e)(x2 – x1), x1 < e < x2
По умові f¢(e)>0, отже, f(x2) – f(x1)>0, тобто функція f(x) зростає.
Теорема доведена.
Аналогічно можна зробити висновок про те, що якщо функція f(x) спадає на відрізку [а, b], то f¢(x)£0 на цьому відрізку. Якщо f¢(x)<0 у проміжку (а, b), то f(x) спадає на відрізку [а, b].
Звичайно, дане твердження справедливе, якщо функція f(x) неперервна на відрізку [а, b] і диференційована на інтервалі (а, b).
 Доведену вище теорему можна проілюструвати геометрично:
Доведену вище теорему можна проілюструвати геометрично:
у у
j j j j
x x
2.Точки екстремуму. Стаціонарні і критичні точки.
Означення: Функція f(x) має в точці х1 максимум, якщо її значення в цій точці більше значень в усіх точках деякого інтервалу, що містить точку х1. Функція f(x) має в точці х2 мінімум, якщо f(x2 +Dx) > f(x2) при будь-якомуDх (Dх може бути і від’ємним).
Очевидно, що функція, визначена на відрізку може мати максимум і мінімум тільки в точках, що знаходяться усередині цього відрізка. Не можна також плутати максимум і мінімум функції з її найбільшим і найменшим значенням на відрізку – це поняття принципово різні.
Означення: Точки максимуму і мінімуму функції називаються точками екстремуму.
Теорема (необхідна умова існування екстремуму-теорема Ферма): Якщо функція f(x) диференційована в точці х = х1 і точка х1 є точкою екстремуму, то похідна функції дорівнює нулю в цій точці.
Доведення.
Припустимо, що функція f(x) має в точці х = х1 максимум. Тоді при достатньо малих позитивних Dх>0 вірна нерівність:  , тобто
, тобто
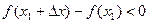 Тоді
Тоді 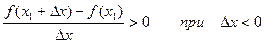
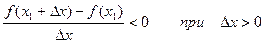
За означенням: 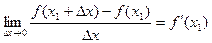
Тобто якщо Dх®0, але Dх<0, то f¢(x1) ³ 0, а якщо Dх®0, але Dх>0, то f¢(x1) £ 0. А можливо це тільки в тому випадку, якщо при Dх®0 f¢(x1) = 0.
Для випадку, якщо функція f(x) має в точці х2 мінімум теорема доводиться аналогічно.
Теорема доведена.
Наслідок: Зворотне твердження невірне. Якщо похідна функції в деякій точці рівна нулю, то це ще не значить, що в цій точці функція має екстремум. Красномовний приклад цього – функція у = х3, похідна якої в точці х = 0 рівна нулю, проте в цій точці функція має тільки перегин, а не максимум або мінімум.
Означення. Критичними точками функції називаються точки, в яких похідна функції не існує або рівна нулю.
Розглянута вище теорема дає нам необхідні умови існування екстремуму, але цього недосить.
Приклад: f(x)= ôxô Приклад: f(x)= 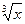
 у у
у у
x
У точці х = 0 функція має мінімум, але В точці х = 0 функція не має ні
не має похідної. максимуму, ні мінімуму, ні
похідної.
Взагалі кажучи, функція f(x) може мати екстремум в точках, де похідна не існує або рівна нулю.
Теорема (достатні умови існування екстремуму – теорема Вейєрштрасса):
Хай функція f(x) неперервна в інтервалі (а, b), який містить критичну точку х1, і диференційована в усіх точках цього інтервалу (окрім, можливо, самої точки х1). Якщо під час переходу через точку х1 зліва направо похідна функції f¢(x) міняє знак з “+” на “-“, то в точці х = х1 функція f(x) має максимум, а якщо похідна міняє знак з “-“ на “+”- то функція має мінімум.
Доведення.
Хай 
По теоремі Лагранжа: f(x) – f(x1)= f¢(e)(x – x1), де x < e < x1.
Тоді: 1) Якщо х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, отже
f(x) – f(x1)<0 або f(x)< f(x1).
2) Якщо х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, отже
f(x) – f(x1)<0 або f(x)< f(x1).
Т. до. відповіді співпадають, то можна сказати, що f(x)< f(x1) в будь-яких точках поблизу х1, тобто х1 – точка максимуму.
Доведення теореми для точки мінімуму - аналогічно.
Лекція 29.
Тема: Найбільше і найменше значення функції на відрізку. Розв’язування прикладних задач на екстремум.
План.
1.Найбільше і найменше значення функції на відрізку.
2. «Екстремальні задачі».
1.Найбільше і найменше значення функції на відрізку.
Нехай 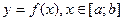 - неперервна, диференційована, має критичні точки І роду. Знайдемо її найбільше та найменше значення на проміжку
- неперервна, диференційована, має критичні точки І роду. Знайдемо її найбільше та найменше значення на проміжку 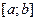 .
.
Зауваження: Якщо 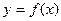 - монотонна на проміжку
- монотонна на проміжку 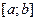 , то при
, то при
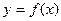 - зростаюча,
- зростаюча, 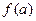 -найменше,
-найменше,  -найбільше;
-найбільше;
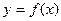 - спадна,
- спадна, 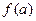 -найбільше,
-найбільше,  -найменше.
-найменше.
Якщо функція 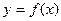 - не монотонна, то свого найбільшого чи найменшого значення вона досягає або в одній з точок екстремуму, або в кінцях відрізка.
- не монотонна, то свого найбільшого чи найменшого значення вона досягає або в одній з точок екстремуму, або в кінцях відрізка.
План знаходження найбільшого і найменшого значення функції 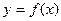 на проміжку
на проміжку 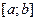 :
:
1. Знайти критичні точки І роду.
2. Обчислити значення функції в усіх критичних точках і на кінцях проміжка.
3. Із одержаних значень вибираєм найбільше і найменше.
Наприклад: Знайти найбільше і найменше значення функції на вказаному проміжку
А) 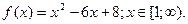
Розв’язання:
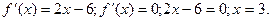
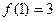 -найбільше;
-найбільше;
 -найменше.
-найменше.
Б) 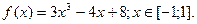
Розв’язання:

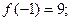
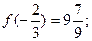 найбільше.
найбільше.
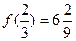 -найменше.
-найменше.
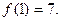
2. «Екстремальні задачі».
Знаходження найбільшого і найменшого значення функції широко застосовується для розв’язування прикладних задач.
Теорема: Якщо функція неперервна на деякому проміжку (відкритому чи закритому) і має єдиний екстремум, то він є її найменшим значенням у випадку мінімуму та найбільшим у випадку максимуму.
Практичного значення набувають не самі максимуми і мінімуми, а значення аргументу, при яких вони досягаються.
План розв’язування прикладних задач:
1. Визначити невідому величину.
2. Скласти функцію.
3. Знайти найбільше і найменше значення функції.
Наприклад: Число 162 представити у вигляді суми 3-х доданків (додатніх) так, щоб одне з них було у 5 раз більше другого, а добуток цих трьох чисел був би найбільшим.
Розв’язання:
Нехай ІІ число х; І 5х; ІІІ 162-(х+5х)=162-6х.
Функція у=f(х)=х*5х*(162-6х) дослідимо на максимум.
у=810х2-30х3; у/=1620х-90х2; у/=0; 1620х-90х2=0; х(1620-90х)=0; х1=0; х2=18.
 |
 + -
+ -
0  18
18  162 х
162 х
max
Відповідь: 18; 90; 54.
Лекція 30.
Тема: Загальна схема дослідження та побудова графіка функції.
Схема дослідження функції і побудова графіка:
1) знайти область визначення;
2) дослідити функцію на парність і непарність;
3) дослідити функцію на періодичність;
4) дослідити функцію на неперервність, знайти точки розриву;
5) знайти критичні точки І роду;
6) знайти інтервали монотонності і екстремуми функції;
7) знайти критичні точки ІІ роду;
8) знайти інтервали опуклості і точки перегину;
9) знайти асимптоти графіка функції;
10) знайти точки перетину графіка функції з осями координат (якщо це можливо);
11) побудувати графік функції.
Наприклад: Побудувати графік функції 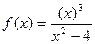 .
.
Розв’язання.
1) Функція визначена для всіх х, крім ±2.
2) Функція непарна, бо 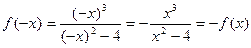 .
.
3) Неперіодична.
4) Неперервна на всій області визначення х=-2, х=2 – точки розриву.
|
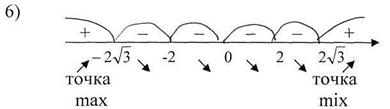
5)  ,
, 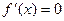 ;
; 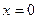 ;
;  , та
, та  не існує при
не існує при 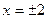 .
.  має критичні точки І роду
має критичні точки І роду 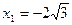 ;
; 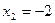 ;
; 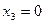 ;
; 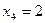 ;
; 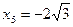 .
.
Мал.53.
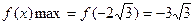 ;
;

7) 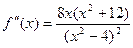 ,
, 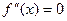 та
та 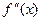 не існує при
не існує при 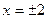 .
.
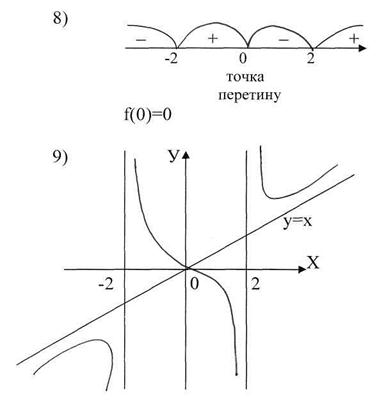
Отже, х2=-2; х3=0, х4=2 –критичні точки ІІ роду.
|
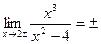
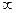 Мал.54.
Мал.54.
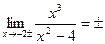
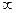
х=-2, х=2 – вертикальні асимптоти.
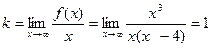 ,
,
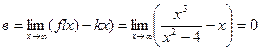 .
.
у=х – похила асимптота.
Лекція 31.
Тема: Первісна, Таблиця первісних. Невизначений інтеграл.
План.
1.Первісна. Основна властивість первісної.
2.Таблиця первісних.
3.Невизначений інтеграл. Таблиця інтегралів.
4.Правила обчислення первісних.
1.Первісна. Основна властивість первісної.
При вивченні теми «Похідна» ми мали задачу про знаходження швидкості прямолінійного руху по заданому закону зміни координати  матеріальної точки. миттєва швидкість
матеріальної точки. миттєва швидкість  дорівнює похідній функції
дорівнює похідній функції  , тт..
, тт..  =
= 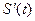 .
.
На практиці зустрічається обернена задача: по заданій швидкості  руху точки знайти пройдений нею шлях
руху точки знайти пройдений нею шлях  , тт.. знайти таку функцію
, тт.. знайти таку функцію  , похідна якої дорівнює
, похідна якої дорівнює  .
.
Означення: Функція  називається первісною для функції
називається первісною для функції  на деякому проміжку, якщо для всіх х із цього проміжку виконується рівність
на деякому проміжку, якщо для всіх х із цього проміжку виконується рівність 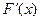 =
=  .
.
Наприклад: Функція  =
= 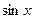 є первісною для функції
є первісною для функції  =
= 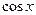 , бо
, бо  .
.
Розглянемо функцію 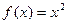 . Доведемо, що функції
. Доведемо, що функції 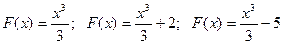 є первісними для функції
є первісними для функції 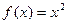 .
.
Дійсно,  .
.
Висновок: Будь-яка функція 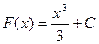 , де С-стала, є первісною для функції
, де С-стала, є первісною для функції 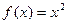 .
.
Теорема: Нехай функція  є первісною для
є первісною для  на деякому проміжку. Тоді для довільної сталої С функція
на деякому проміжку. Тоді для довільної сталої С функція 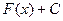 також є первісна для функції
також є первісна для функції  .
.
Доведення:
 -первісна для
-первісна для  , тт.
, тт.  . Тоді
. Тоді 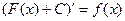 .
. 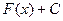 є первісна для
є первісна для  .
.
Теорема: Нехай функція  є первісною для
є первісною для  на деякому проміжку. Тоді будь-яка первісна для функції
на деякому проміжку. Тоді будь-яка первісна для функції  на цьому проміжку може бути записана у вигляді
на цьому проміжку може бути записана у вигляді 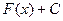 , С-стала.
, С-стала.
Доведення:
Нехай  і
і 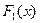 -дві первісні для однієї функції
-дві первісні для однієї функції  , тт.
, тт.  і
і  . Отже, похідна різниці
. Отже, похідна різниці 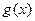 =
=  -
- 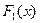 дорівнює 0.
дорівнює 0.
Якщо похідна 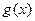 дорівнює нулю, то дотична до графіка функції
дорівнює нулю, то дотична до графіка функції 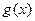 в кожній точці проміжка паралельна осі ОХ, тт.. графік функції
в кожній точці проміжка паралельна осі ОХ, тт.. графік функції 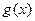 -пряма, паралельна ОХ, тт..
-пряма, паралельна ОХ, тт.. 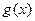 =С, С-стала величина.
=С, С-стала величина.  -
- 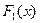 =С,
=С, 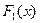 =
=  +С.
+С.
Ці теореми виражають основну властивість первісної. Основній властивості первісної можна надати геометричного змісту: графіки будь-яких двох первісних для функції  одержуються один з одного паралельним перенесенням вздовж осі ОУ.
одержуються один з одного паралельним перенесенням вздовж осі ОУ.
2.Таблиця первісних.
функція

| 
| 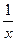
| 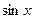
| 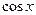
| 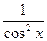
| 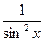
| 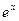
| 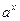
| ||
первісна
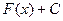
| С | 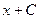
| 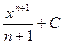
| 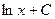
| 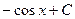
| 
| 
| 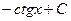
| 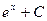
| 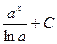
|
3.Невизначений інтеграл. Таблиця інтегралів.
Нехай функція  на деякому проміжку має первісну. Сукупність усіх первісних функції
на деякому проміжку має первісну. Сукупність усіх первісних функції  на проміжку називають невизначеним інтегралом цієї функції і позначають
на проміжку називають невизначеним інтегралом цієї функції і позначають 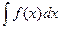 . Функцію
. Функцію  називають підінтегральною функцією.
називають підінтегральною функцією.
З основної властивості первісної маємо 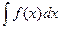 =
= 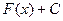 .
.
Таблиця інтегралів.
1) 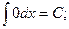 2)
2) 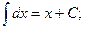
3) 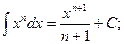 4)
4) 
5)  6)
6) 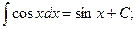
7) 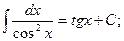 8)
8) 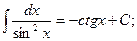
9) 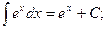 10)
10) 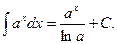
4.Правила обчислення первісних.
Операція знаходження первісних – інтегрування. Правила інтегрування можна одержати за допомогою правил диференціювання.
1) Первісна суми функцій дорівнює сумі первісних.
Доведення: Оскільки,  і
і 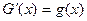 , то
, то 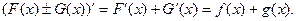
Це правило можна сформулювати в іншій формі: інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів:
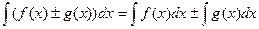 .
.
Наприклад: Знайти первісну для функції 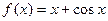 .
.
Розв’язання:
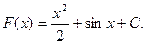
2) Якщо  - первісна для
- первісна для  , С – стала, то
, С – стала, то 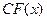 - первісна для функції
- первісна для функції 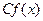 .
.
Доведення: Оскільки,  , то
, то 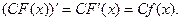
Сталий множник можна виносити за знак інтеграла: 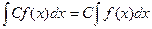 .
.
Наприклад: Знайти первісні для функції 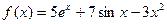 .
.
Відповідь: 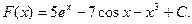
3) Якщо  - первісна для
- первісна для  , а
, а 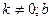 - числа, то
- числа, то 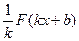 - первісна для функції
- первісна для функції  .
.
Доведення: 
В інтегральній формі 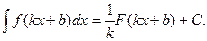
Наприклад: Знайти первісні 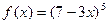 .
.
Відповідь: 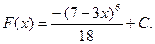
Лекція 32.
Тема: Приклади задач, що приводять до поняття інтеграла.Визначений інтеграл. Формула Ньютона-Лейбніца.
План.
1.Задача про площу криволінійної трапеції.
2.Задача про знаходження шляху, пройденого тілом.
3.Поняття інтеграла.
4.Формула Ньютона – Лейбніца.
1.Задача про площу криволінійної трапеції.
Криволінійною трапецією називається фігура, обмежена графіком неперервної функції  , яка не змінює знак на відрізку
, яка не змінює знак на відрізку  , прямими
, прямими 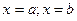 і відрізком
і відрізком  .
.


 y
y


 у
у





 | |||
 |
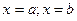 х x0=а х1 х2 хn-2 xn-1 b=xn x
х x0=а х1 х2 хn-2 xn-1 b=xn x
Нехай треба обчислити площу криволінійної трапеції. Розіб’ємо відрізок  на
на  рівних частин і позначимо точки поділу через x0=а, х1, х2 … хn-2 , xn-1, b=xn. На кожному із цих відрізків побудуємо прямокутники, висотою
рівних частин і позначимо точки поділу через x0=а, х1, х2 … хn-2 , xn-1, b=xn. На кожному із цих відрізків побудуємо прямокутники, висотою 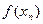 . Довжина основи кожного прямокутника дорівнює
. Довжина основи кожного прямокутника дорівнює 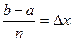 . Об’єднання цих прямокутників є східчаста фігура. Позначимо її площу через
. Об’єднання цих прямокутників є східчаста фігура. Позначимо її площу через 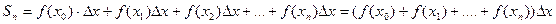 . Якщо
. Якщо 
 - неперервна, то східчаста фігура буде все менше відрізнятися від криволінійної трапеції, тт.
- неперервна, то східчаста фігура буде все менше відрізнятися від криволінійної трапеції, тт.  . При досить великих
. При досить великих  ця наближена рівність справджується з великою точністю. Вважають, що
ця наближена рівність справджується з великою точністю. Вважають, що  при цьому буде наближатися до числа, яке приймемо за значення площі криволінійної трапеції,
при цьому буде наближатися до числа, яке приймемо за значення площі криволінійної трапеції, 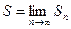 .
.
2.Задача про знаходження шляху, пройденого тілом.
Між координатою точки і її швидкістю існує зв’язок 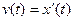 .
.
Нехай точка рухається з постійною швидкістю 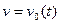 . Графіком швидкості в системі координат
. Графіком швидкості в системі координат  буде пряма
буде пряма 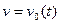 паралельна осі часу. Якщо вважати, що в початковий момент часу
паралельна осі часу. Якщо вважати, що в початковий момент часу  точка знаходиться в початку координат, то шлях її
точка знаходиться в початку координат, то шлях її 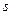 , пройдений за час
, пройдений за час  обчислюється за формулою
обчислюється за формулою 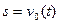 , це площа прямокутника, обмеженого графіком швидкості, віссю часу і двома вертикальними прямими, тт. шлях можна обчислити як площу криволінійної трапеції.
, це площа прямокутника, обмеженого графіком швидкості, віссю часу і двома вертикальними прямими, тт. шлях можна обчислити як площу криволінійної трапеції.
Звернемося до випадку нерівномірного руху. Швидкість вважається постійною на маленькому проміжку часу. Розіб’ємо проміжок часу 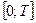 на
на  рівних частин
рівних частин 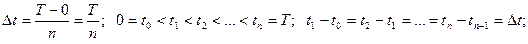
Шлях, пройдений тілом за час  приблизно дорівнює добутку
приблизно дорівнює добутку  , а шлях, пройдений тілом за проміжок часу
, а шлях, пройдений тілом за проміжок часу 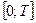 становить
становить 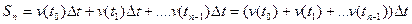 ; якщо
; якщо 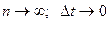 , то шлях, пройдений тілом за проміжок часу
, то шлях, пройдений тілом за проміжок часу 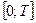
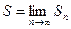 .
.
3.Поняття інтеграла.
За зразком розглянутих задач можна знайти роботу змінної сили, масу неоднорідного стержня та ін. Узагальнимо цей спосіб розв’язку задач.
Розглянемо неперервну функцію  , яка не змінює знак на відрізку
, яка не змінює знак на відрізку  . Розіб’ємо відрізок
. Розіб’ємо відрізок  на
на  рівних частин і позначимо точки поділу через x0=а, х1, х2 … хn-2 , xn-1, b=xn. Довжина кожного відрізка дорівнює
рівних частин і позначимо точки поділу через x0=а, х1, х2 … хn-2 , xn-1, b=xn. Довжина кожного відрізка дорівнює 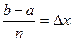
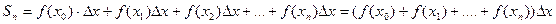 . Якщо
. Якщо 
 - неперервна, тт.
- неперервна, тт.  .
. 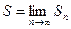 .
.
За означенням цю границю називають інтегралом функції  від
від 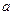 до
до 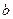 і позначають
і позначають 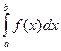 .
.
У позначенні інтеграла все вказує на спосіб його утворення. Знак інтеграл нагадує видовжену латинську літеру  - першу букву слова summa (сума). Так,
- першу букву слова summa (сума). Так, 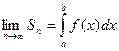 .
.
4.Формула Ньютона – Лейбніца.
Площу криволінійної трапеції можна обчислити за допомогою первісної функції.
Позначимо  площу криволінійної трапеції з основою
площу криволінійної трапеції з основою 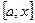 , де х – точка з відрізка
, де х – точка з відрізка  . Якщо х=а, то
. Якщо х=а, то  =0, якщо х=
=0, якщо х= 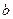 , то
, то 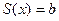 .
.
Площу криволінійної трапеції можна обчислити за формулою
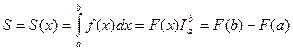 -формула Ньютона-Лейбніца.
-формула Ньютона-Лейбніца.
Лекція 33: Застосування інтегралів до обчилення площ плоских фігур та
Поиск по сайту: