Пример 3.2

Положительный заряд q = 5 × 10^-8 Кл равномерно распределен по тонкому проволочному полукольцу радиуса R= 20 см. Определить напряженность поля Е в центре полукольца.

Дано:

q = 5 × 10^-8 Кл;

R = 20 см;

e = 1

Е –?

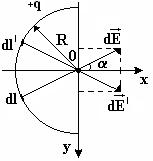Анализ и решение: В этой задаче поле создается зарядом q, распределенным по тонкому полукольцу радиуса R. Линейная плотность заряда равна: 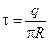. Для такого случая нельзя непосредственно воспользоваться формулой напряженности для поля точечного заряда или бесконечной заряженной нити. Такую задачу можно решить, используя принцип суперпозиции. Разделим весь проводник на очень маленькие участки длиной dl, на каждый из которых приходится заряд dq =t × dl. Такой заряд можно считать точечным и величину напряженности поля этого заряда рассчитать по формуле

.

На рисунке показан выбор осей координат и вектор напряженности поля 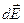, создаваемый в точке О зарядом 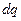.Учитывая симметрию задачи, удобно начало отсчёта системы координат связать с точкой О, центром полукольца, и направить оси координат так, как изображено на рисунке.

Спроектируем вектор 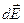на оси координат:

dЕ _x = dE × cosa;

dE _y = dE × sina.

Из симметрии видно, что каждому элементарному заряду dq найдется симметрично расположенный относительно оси ОХ заряд dq ¢. Проекции напряженностей полей этих зарядов на ось ОУ дадут ноль при любых углах a.

Таким образом, надо найти только проекцию суммарного вектора на ось ОХ. Понятно, что в случае непрерывного распределения заряда суммирование следует заменить интегрированием по всей длине проволоки, на которой расположен заряд.

.

В подынтегральное выражение входят две переменные l и a. Учитывая, что 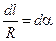и dl = Rd a, заменим переменную интегрирования и получим

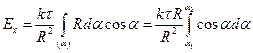
или

.

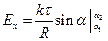Из рисунка видно, что 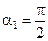, а .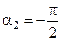

Окончательно получаем

;

; .

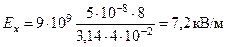Ответ: напряженность поля в центре кольца равна 7,2 кВ/м.

Поиск по сайту: