Подставим в теорему Гаусса полученные выражения для потока вектора напряженности и суммарного заряда

Запишем теорему Гаусса в общем виде .

Для каждой из рассматриваемых областей пространства мы получили выражения для потока вектора напряженности электрического поля и формулы для вычисления заряда, охватываемого поверхностью интегрирования. Вся система зарядов находится в воздухе, поэтому для всех трех случаев электрическая постоянная равна единице ().

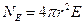
Для получения искомой зависимости 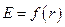рассмотрим три выделенные области и запишем для них теорему Гаусса:

I область П область Ш область

Из этих уравнений получим зависимость для каждой области:

.

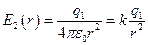
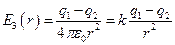6. Получим количественный результат для точек, указанных в условии задачи (r ₁ = 5 см, r ₂ = 9 см и r ₃ = 15 см).

Напряженность поля в точке, находящейся на расстоянии r ₁ = 5 см будет равна нулю, т.к. точка лежит в первой из рассмотренных областей:

Вторая точка находится во второй области. Подставим численные значения:

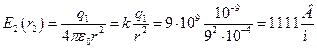
Для третьей точки получаем:

7. Построим график зависимости величины напряженности Е электрического поля заряженных сфер от расстояния от рассматриваемой точки до центра сферических поверхностей .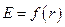

Мы получили три функции для трех областей пространства:

; ; .

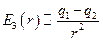Из полученных выражений видно, что в первой области напряженность поля постоянна и равна нулю; во второй и третьей областях зависимость от расстояния представляет собой квадратичную гиперболу, но числители функций различны.Для построения графика получим численные значения напряженности поля в некоторых 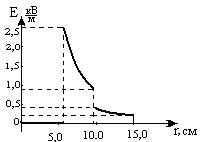точках:

.

Учитывая полученные значения, выберем масштаб и нарисуем график полученной зависимости.

Пример 3.2.2. Имеется плоскопараллельная пластина толщиной d = 3 см равномерно заряженная по объему с плотностью r = 2×10^-8 Кл/м³. Диэлектрическая проницаемость материала пластины e=2.

1) Используя теорему Гаусса найдите напряженность электрического поля внутри пластины и вне нее, как функцию расстояния от центра пластины.

2) Постройте график зависимости .

Дано:

d = 3 см

r = 2×10^-8 Кл/м³;

r ₁ = 1 см;

r ₂ = 3см;

Е = f (r) =?

Анализ: Задачи о вычислении напряженности поля, создаваемого симметричным распределением заряда, решаются с использованием теоремы Гаусса. Формулировка теоремы: поток вектора напряженности электрического поля через замкнутую поверхность равняется алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрические постоянные.

, где .

Угол α – это угол между вектором и вектором нормали к поверхности интегрирования .

При применении теоремы Гаусса для расчета напряженности поля некоторого заряженного тела удобно действовать по определенному алгоритму.

1. Необходимо нарисовать картину силовых линий заданного распределения зарядов.

В нашей задаче пластину считаем бесконечно протяженной, и поэтому в каждой точке пространства напряженность поля будет направлена перпендикулярно пластине. Силовые линии будут представлять собой параллельные прямые, перпендикулярные пластине. Начало оси координат выбираем в средней точке пластины, а саму ось направляем вдоль силовых линий

2. Выбрать поверхность интегрирования, учитывая симметрию задачи, таким образом, чтобы силовые линии поля либо скользили по поверхности, либо были ей перпендикулярны.

Учитывая симметрию задачи, выбираем замкнутую поверхность в виде цилиндра радиуса R и высотой H (можно было бы и в виде прямоугольного параллелепипеда). Рисунок выполнен в сечении, перпендикулярном самой заряженной пластине. Сечение выбранной поверхности изображено прерывистой линией. Нарисовано два цилиндра, оси которых совпадают с силовыми линиями электростатического поля, для двух случаев определения напряженности поля - внутри и вне пластины. Основания цилиндров симметричны относительно середины пластины. Точка, в которой мы хотим вычислить величину вектора Е должна находится на основании цилиндра.

3. Вычислим поток вектора через выбранную поверхность.

Полный поток можно сосчитать как сумму потоков через два основания цилиндра и через его боковую поверхность

.

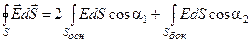Как видно из рисунка, a₁ = 0⁰, а a₂ = 90⁰, следовательно, поток отличен от нуля только для двух оснований.

С учетом этого получим

.

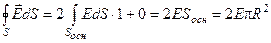Перед первым интегралом стоит множитель «2», т.к. два основания симметрично расположены и модуль вектора Е на равных расстояниях от пластины будет одинаков, поэтому его можно вынести за знак интеграла.

4. Запишем выражение для заряда, охватываемого этой поверхностью.

.

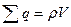а). Если искомая точка лежит внутри пластины, то V = S _осн2 r, где r – расстояние от центра пластины. Поверхность интегрирования вся расположена внутри пластины. .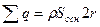

б). Если искомая точка лежит вне пластины, то V = S _осн d. Высота поверхности интегрирования Н больше толщины пластины d. Заряд находится только внутри пластины. .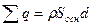

5. Воспользуемся теоремой Гаусса:

Подставим выражения, полученные в пунктах 3 и 4 в левую и правую части теоремы. .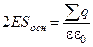

Из полученного уравнения можно получит формулу, дающую зависимость напряженности поля Е от расстояния r до центра пластины.

а) Внутри пластины применение теоремы Гаусса приводит к уравнению 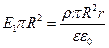, из которого получаем искомую зависимость - напряженности поля внутри пластины от расстояния r. e – диэлектрическая проницаемость материала заряженной пластины, по условию e = 2. Полученная зависимость – линейная, т.е. напряженность поля прямо пропорциональна расстоянию r.

б) Вне пластины получили следующее уравнение 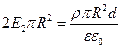. В этом случае получаем следующую зависимость - напряженность поля вне пластины. Пластина находится в воздухе; Диэлектрическая проницаемость для воздуха равна единице. Величина напряженности поля вне пластины не зависит от расстояния r, как видно из формулы. Следовательно поле однородное.

Построим график зависимости Е от r. Внутри пластины напряженность поля линейно возрастает с увеличением r. Вне пластины поле однородное. Проекции вектора на ось имеют разные знаки, поскольку силовые линии направлены от центра пластины в противоположные стороны.

Скачок значения напряженности при
r = ±d/2 происходит из-за изменения диэлектрической проницаемости среды. Внутри пластины она равна e₁ = 2, а вне нее e₂ = 1, поэтому напряженность поля скачком увеличивается в два раза.

Поиск по сайту: