АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Несобственные интегралы второго рода

Читайте также:
  1. Аналитическое выравнивание по параболе второго порядка
  2. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  3. Вопрос об открытии второго фронта
  4. Вторая фаза Второго русского Востока (1241–1253)
  5. Двойные и криволинейные интегралы
  6. Задачи второго класса
  7. Законы организации второго уровня
  8. Инерционные звенья второго порядка
  9. Инерционные звенья второго порядка
  10. Интегралы Лагранжа и Эйлера
  11. Ищущие второго типа, правильные ищущие, они не занимаются поисками того, что делать, они в поисках того, как жить, как существовать. Главным является то, как жить.
  12. Линейные уравнения второго порядка с постоянными коэффициентами

В этом параграфе будет дано обобщение понятия определенного интеграла на случай неограниченных функций.

Пусть на полусегменте задана функция f(x). Точку b мы будем называть особой, если функция не ограничена наполусегменте , но ограничена на любом сегменте , заключенном в полусегменте . Будем также предпола­гать, что на любом таком сегменте функция f(х) интегрируема. При наших предположениях на полусегменте задана функция аргумента

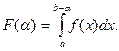
Исследуем вопрос о правом пределе функции в точке =0

(3.1)

Определение3. Правый предел (1.14) в случае, если он существует, называется несобственным интегралом второго рода от функции f(х) по сегменту [ а, b ] и обозначается символом

(3.2)

При этом говорят, что несобственный интеграл (3.2) сходится и пишут равенство

=

Символ (3.2) употребляют и в случае, если указанного выше предела (3.1) не существует, но в этом случае говорят, что несобственный интеграл (3.2) расходится.

Замечание. Понятие несобственного интеграла второго рода легко переносится на случай, когда функция f(х) имеет конечное число особых точек.

Пример. Рассмотрим на полусегменте [ а, b) функцию Ясно, что точка b является особой точкой для этой функции. Кроме того, очевидно, что эта функция интегрируема на любом сегменте , , причем

Очевидно, предел существует и равен

при и не существует при . Следовательно, рассматриваемый несобственный интеграл сходится при и расходится при .

Сформулируем критерий Коши сходимости несобственного интеграла второго рода. При этом мы будем предполагать, что функция f(х) задана на полусегменте и b — особая точка этой функции.

Утверждение 5. (критерий Коши). Для сходимости несобственного интеграла второго рода (3.2) необходимо и достаточно, чтобы, для любого можно было указать такое , что для любых и , удовлетворяющих условию 0< < , справедливо неравенство

 

Замечания.

1°. При некоторых ограничениях на подынтегральные функции интегралы второго рода сводятся к интегралам первого рода. Именно: пусть функция f(х) непрерывна на полусегменте и b — особая точка этой функции. При этих условиях в интеграле , мы можем произвести следующую замену переменных:

В результате этой замены переменных мы получим равенство

(3.3)

Пусть интеграл 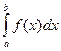сходится. Это означает, что существует предел Обращаясь к равенству (3.3) мы видим, что существует также и предел при выраже­ния в правой части (3.3) Тем самым доказана сходимость не­собственного интеграла первого рода

и равенство этого интеграла интегралу 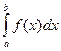. Очевидно сходимость только что указанного несобственного интеграла первого рода влечет сходимость интеграла 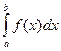и равенство этих интегралов. Итак, из сходимости одного из интегралов

следует сходимость другого и равенство этих интегралов.

2°. Для несобственных интегралов второго рода легко доказываются утверждения, аналогичные утверждениям для несобственных интегралов первого рода, которые можно объединить общим наименованием «признаки сравнения». Отметим, что во всех формулировках функция f(х) рассматривается на полусегментах [ а,b), где b — особая точка функции.

Частный признак сравнения будет иметь следующий вид.

Если 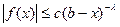,где , то несобственный интеграл (3.1) сходиться. Если же , где и несобственный интеграл (3.1) расходится. Доказательство вытекает из общего признака сравнения и примера, рассмотренного выше.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)