Волновая функция электронов в кристалле

Во многом отличия в физико-химических свойствах металлов, полупроводников и диэлектриков в значительной мере обусловлены существованием фундаментальных различий в их зонной структуре, в степени заполнения валентных зон электронами и в значениях ширины разрешенных зон электронов и разделяющих их промежутков (запрещенных зон). Зонная модель твердого тела вытекает из решения уравнения Шредингера для электронов в кристалле. Цель данной лекции, показать, в чем заключается специфика электронной структуры твердых тел, обусловленная их зонным строением и характеризуемая уравнением Шредингера:

Ĥ Y = Е Y, (1.1)

где Ĥ – гамильтониан кристалла, Y - его собственная волновая функция, Е – энергия кристалла.

Волновая функция кристалла зависит от координат всех электронов (r_i) и всех ядер (R_a)

Y = Y (r₁, r₂, … r_n; R₁, R₂, … R_n). (1.2)

Гамильтониан включает операторы, характеризующие кинетическую энергию электронов (T_i) и ядер (T_z), потенциальную энергию электронов (U_i) и ядер (U_z), энергию парных взаимодействий электронов и ядер между собой (U_iz)

Ĥ = T_i + T_z + U_i + U_z + U_iz; (1.3)

T_i = = , где (1.4)

; (1.5)

T_z = ; (1.6)

U_i = ; (1.7)

U_iz = ; (1.8)

Уравнение с таким гамильтонианом содержит 3N(z+1) переменных, где N – число атомов в кристалле. Учитывая, что в 1 см³ кристалла в среднем содержится 5 × 10²² атомов, при z = 14 число переменных составляет огромную величину, порядка 2 × 10²⁴. Очевидно, что решить такое уравнение невозможно, и поэтому вводятся различного рода приближения и, в первую очередь, адиабатическое приближение.

В рамках этого приближения, называемого приближением Борна – Оппенгеймера, кристалл разделяется на две подсистемы – “медленную”, связанную с движением ядер (“тяжелых” частиц) и “быструю” – электронную. Считается, что движение “тяжелого” ядра в силу его инерционности не зависит от движения каждого “легкого” электрона, и поэтому ядро движется в усредненном поле всех электронов. С другой стороны, относительно медленно движущееся ядро увлекает за собой электроны (условие сохранения целостности атомов, составляющих кристалл).

В простейшем случае принимаем, что ядро вообще неподвижно, то есть . В этом случае кинетическая энергия ядер , а энергия их взаимодействия между собой , которую можно обратить в нуль соответствующим сдвигом точки отсчета энергии. В итоге, гамильтониан для электронов упрощается

Ĥ = T_i + T_z + U_i, (1.9)

и уравнение Шредингера приобретает вид:

, (1.10)

где - координаты покоящихся ядер (параметр, а не переменная).

С целью дальнейшего сокращения числа переменных в уравнении Шредингера принимается, что все электроны, входящие в состав атома, за исключением валентных электронов, вместе с ядром образуют положительно заряженный неподвижный ион (не следует путать с традиционным понятием “ион” в растворах и ионных кристаллах). Эти ионы формируют остов кристалла (“медленную” подсистему), а валентные электроны, соответственно, “быструю” подсистему. Соответственно, в уравнении Шредингера рассматривается движение валентных электронов в потенциальном поле фиксированных ионов (валентная аппроксимация).

Переход от рассмотрения многоэлектронной системы к одноэлектронной (с учетом движения только валентных электронов) осуществляется в рамках метода Хартри-Фока, в котором энергия попарного взаимодействия электронов заменяется энергией взаимодействия каждого электрона с усредненным полем всех остальных электронов:

, (1.11)

где - потенциальная энергия отдельно взятого электрона в поле всех остальных электронов. В этом соотношении важно, что двойная сумма (по и ) заменяется на сумму, каждый из членов которой зависит от координат одной частицы. Тогда волновая функция системы частиц может быть представлена как произведение волновых функций, описывающих состояние отдельных частиц системы:

Y = Y₁Y₂Y₃ ××× Y_n, (1.12)

и это означает, что электроны ведут себя независимо друг от друга, а полная энергия системы частиц равна сумме энергий отдельных электронов:

E_e = E₁ + E₂ + … = E_i. (1.13)

Таким образом, введение самосогласованного поля позволяет рассматривать электроны в кристалле движущимися независимо друг от друга. Это является также и определенным основанием для представления электронов проводимости в виде идеального газа.

Волновая функция электронов в кристалле определяется, в первую очередь, характером взаимодействия валентных электронов с периодическим потенциалом решетки.

Рассмотрим вид волновой функции электрона, находящегося в поле с периодическим потенциалом кристаллической решетки. Поскольку точки с радиус-вектором и физически эквивалентны (ввиду наличия периодичности кристалла: ), очевидно, что . Соответственно, волновая функция 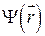отличается от лишь постоянным множителем:

, (1.14)

причем из условия нормировки следует, что .

Из этого условия можно получить как тривиальный вывод (), так и решение в форме

. (1.15)

Геометрически такое решение может быть представлено как круговое движение из некоторой произвольной точки по циклической решетке с возвратом в исходную точку. Комбинируя уравнения (1.14) и (1.15), получаем:

. (1.16)

Умножая правую часть этого уравнения на exp(ikr) × exp(-ikr) (фактически, на единицу) и комбинируя экспоненты и , получаем:

, где (1.17)

. (1.18)

Таким образом, волновая функция электрона в кристалле, называемая функцией (или волной) Блоха имеет вид:

, (1.19)

где - периодический (с периодом решетки) множитель, характеризующий взаимодействие волновой функции электрона с остовами (ионами) решетки, а - бегущая плоская волна свободного электрона с волновым вектором в направлении .

Поиск по сайту: