Энергетическое распределение электронов в кристалле; зоны Бриллюэна

Идеальный кристалл бесконечен, состоит из элементарных ячеек, заполняющих без промежутков все его пространство, и обладает регулярной периодической структурой. Кристаллическая решетка - совокупность точек (узлов), связанных тремя некомпланарными векторами трансляций a, b, c:

T = n₁ a + n₂ b + n₃ c, (3.1)

где n₁, n₂, n₃ - целые числа.

В частном случае решетка может быть двумерной либо одномерной, характеризуемой двумя либо одним базисным вектором, соответственно. Параллелепипеды (для трехмерной решетки) и параллелограммы (для двумерной), построенные на векторах трансляции образуют элементарную ячейку решетки, причем для удобства используется комбинация наиболее коротких векторов. В ряде случаев целесообразно построение элементарной ячейки таким образом, чтобы она охватывала область пространства, которая была бы ближе к данному узлу, чем к любому другому трансляционно-эквивалентному узлу (ячейка Вигнера-Зейтца) - рис. 3.1.

Для этого необходимо выбрать некоторый узел (далее он считается центральным) и соединить его линиями со всеми соседними узлами. Перпендикулярные плоскости, проведенные через середины соединяющих отрезков, образуют ячейку Вигнера-Зейтца (рис. 3.1). Такая ячейка имеет ту же точечную симметрию, что и решетка Браве кристалла, и, естественно, при трансляции заполняет все пространство кристалла без промежутков.

Рис. 3.1. Ячейка Вигнера-Зейтца для квадратной, треугольной и кубической решеток.

Если кристаллическую точечную решетку представить в виде ( - вектора элементарной ячейки, - целые числа), то обратная решетка будет иметь вид:

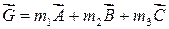, (3.2)

где - целые числа, а векторы находятся из соотношений:

(3.3)

Таким образом, векторы - это основные векторы обратной решетки. В соотношения типа (3.3) кристаллографы обычно опускают множитель , но в теории твердого тела он используется по аналогии с множителем при переходе от обычной частоты к круговой ().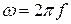

Переход от кристаллической решетки к обратной имеет достаточно сложный физический смысл – фактически мы переходим к пространству частот (величина a^-1 характеризует пространственную частоту решетки).

Таким образом, кристалл может быть охарактеризован частотным параметром (вектором обратной решетки – так называемым k -вектором, равным k = 2π/λ, и обозначающим число волн, укладывающихся на длине 2π, см). Очевидно, что для двух- и трехмерного кристалла пространственные частоты по разным направлениям могут быть различными.

Для рассмотрения состояния электронов в реальном кристалле необходимо найти способ учета его конечных размеров, то есть ввести определенные граничные условия. Чтобы устранить нарушение трансляционной симметрии на краях кристалла и ограничить число структурных единиц в нем можно использовать циклические граничные условия Борна-Кармана. В частности, для ограниченного кристалла в форме параллелепипеда с размерами по осям x, y, z равными, соответственно, L_x, L_y, L_z, составленного из элементарных кубических ячеек можно записать:

L_x = aN_x; L_y = aN_y; L_z = aN_z, (3.4)

где N_x, N_y, N_z - число атомов, укладывающихся на каждом из ребер кристалла. Задавая тождественность волновой функции на противоположных гранях параллелепипеда, получаем граничные условия цикличности Борна-Кармана:

Ψ (x, y, z) = Ψ (x + L_x, y + L_y, z+ L_z). (3.5)

Учитывая, что волновая функция электрона в кристалле имеет вид волны Блоха, для выполнения данных условий цикличности необходимо принять, что:

exp(ik_xL_x) = exp(ik_yL_y) = exp(ik_zL_z) = 1. (3.6)

Такое равенство имеет место при условии, что показатель экспоненты является целым числом, умноженным на 2πi, то есть:

k_xL_x = 2πn₁, k_yL_y = 2πn_2, k_zL_z = 2πn₃, (3.7)

где n₁, n₂, n₃, - целые произвольные числа. Из этого следует, что

k_x = 2πn₁/L_x, k_y = 2πn₂/L_y, k_z = 2πn₃/L_x. (3.8)

Из соотношения (3.8) видно, что компоненты волнового вектора k изменяются не непрерывно, а принимают ряд дискретных значений. Принимая во внимание, что L_x = aN_x, можно заключить, что компонента k_x имеет N_x значений, соответствующих различным значениям n₁, причем оно изменяется в пределах

0 ≤ n₁ < N_x или -N_x/2 ≤ n₁ < N_x/2. (3.9)

Из этих соотношений вытекает, что компоненты вектора k существуют в следующих интервалах:

- π/a ≤ k_x < π/a, - π/a ≤ k_y < π/a, - π/a ≤ k_z < π/a, (3.10)

где k_x, k_y, k_z принимают соответственно N_x, N_y, N_z различных значений.

Таким образом, в рассматриваемой квантовохимической системе содержится всего N = N_xN_yN_z = L_xL_yL_z/a³ различных компонентов вектора k, равное числу элементарных ячеек в кристалле. Это, в принципе, означает, что если каждому значению вектора k будет сопоставлено определенное значение энергии электрона, то в простой энергетической зоне, возникшей из невырожденного атомного уровня, имеется 2N квантовых состояний, и, соответственно N энергетических уровней.

Фактически, компоненты k - вектора k_x, k_y, k_z являются тремя квантовыми числами, а четвертым квантовым числом является спиновое число – s_z. Поскольку проекция s_z может принимать только два значения +1/2 и -1/2, понятно, что в состоянии с одним набором трех компонентов k_x, k_y, k_z может быть не более двух электронов.

Состояние электрона, свободно движущегося в пространстве, характеризуется энергией E и импульсом P, причем E = P² / 2m как и в ньютоновской механике.

С другой стороны, длина волны де Бройля равна λ = h / P, где h - постоянная Планка. Учитывая, что P = mv, а k = 2π / λ, получаем, что импульс электрона P = ħk, где ħ = h / 2π, а энергия E = ħ²k² / 2m.

Для электрона, движущегося в периодическом поле кристалла, понятие импульса существенно изменяется, поскольку параметры движения становятся сильно зависящими от воздействия периодического потенциала остовных ионов. В связи с этим вводится понятие квазиимпульса p = ħk, который квантован в соответствии с дискретным спектром волнового вектора k.

Таким образом, в энергетической зоне кристалла имеется N энергетических состояний, которым соответствуют значения компонент волнового вектора k_i = 2πn_j / L_i и компонент квазиимпульса p_i = 2πħn_j / L_i, где i = x, y, z, а j = 1, 2, 3.

Для кристалла с простой кубической решеткой достаточно рассматривать изменение компонентов k_i и p_i в пределах - π/a ≤ k_i < π/a и - πħ/a ≤ p_i < πħ/a. Этим значениям квазиимпульса в системе координат p_x, p_y, p_z будет соответствовать некоторая область, построенная вокруг начала координат и содержащая все возможные различные состояния. Эта область называется первой (основной) зоной Бриллюэна. Ее можно также определить как ячейку Вигнера-Зейтца в обратной решетке.

В заключение этого раздела рассмотрим кратко основные принципы расчета электронной структуры твердых тел.

Для решения уравнения Шредингера, описывающего состояние электронов в твердом теле, его можно разложить в ряд по полной системе функций, удовлетворяющих тем же граничным условиям, что и искомое решение, причем в упрощенном варианте можно ограничиться конечным набором этих функций:

. (3.11)

Учитывая, что волновая функция электрона в кристалле (функция Блоха) вблизи атомных остовов ведет себя подобно атомной функции , а на удалении от остовов, как набор плоских волн , для разложения уравнения Шредингера можно использовать как сферические волны , так и плоские волны .

В первом случае методы расчета зонной структуры твердого тела относят к методам ячеек, во втором – к вариационным методам.

Поиск по сайту: