Обратная матрица. Ответ: Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если

Ответ: Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если .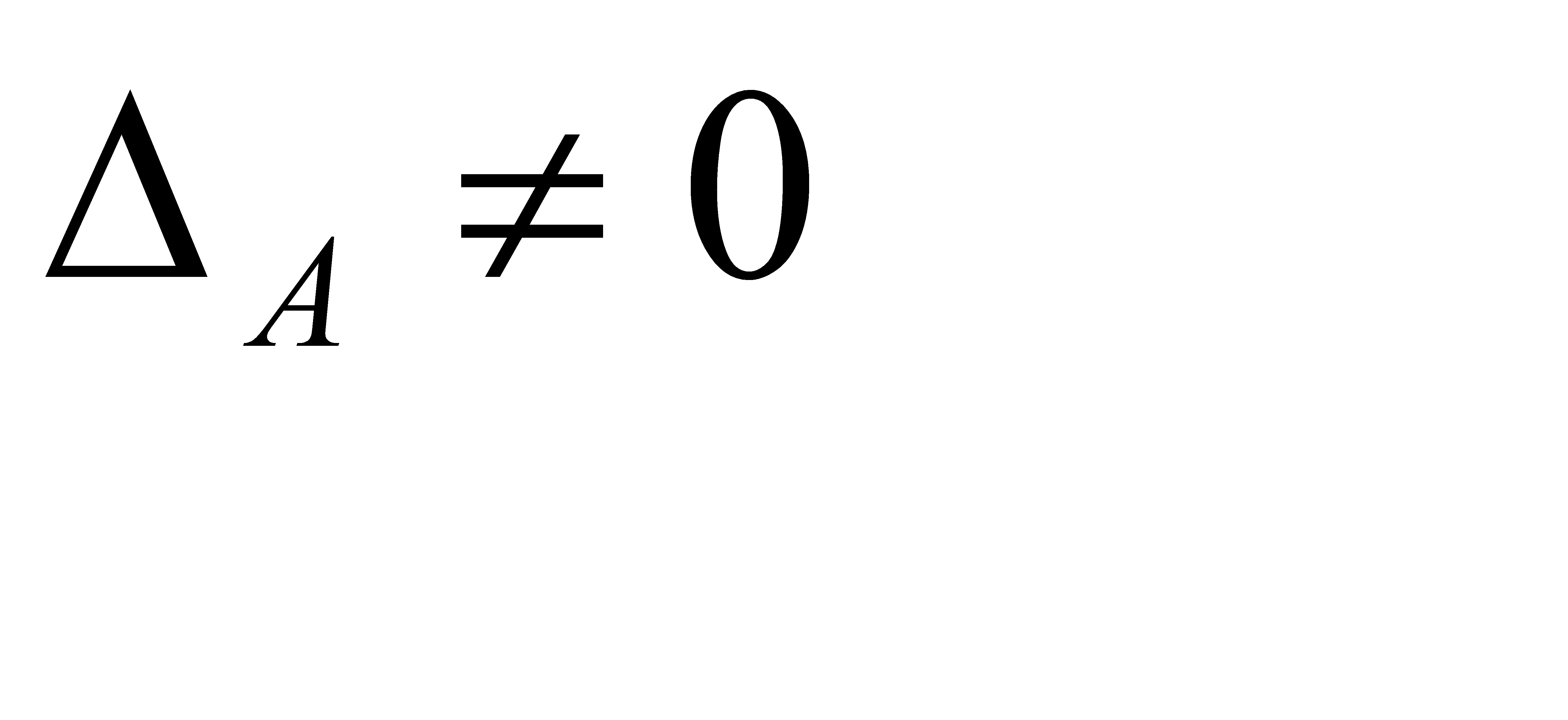

Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.

Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Доказательство.

1) Необходимость: так как то (теорема 3.1), поэтому

2) Достаточность: зададим матрицу в следующем виде:

.

Тогда любой элемент произведения (или ), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны Таким образом,

= . Теорема доказана.

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Пример.

Найдем матрицу, обратную к

следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:

Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, Можно убедиться, что найденная матрица действительно удовлетворяет определению Найдем

Тот же результат получим и при перемножении в обратном порядке.

Поиск по сайту: