 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнения, ограничивающие движение, называются уравнениями связи
Число степеней свободы равно числу координат, определяющих положение точки или системы, минус число уравнений связи.
Одновременное задание в момент времени t обобщённых координат и скоростей обеспечивает возможность полного описания механической системы. В аналитической механике сформулировано в виде постулата следующее положение, известное как принцип наименьшего действия, который гласит:
Существует некоторая функция координат, скоростей и времени 
, которая полностью характеризует механическую систему. Тогда, если в момент времени t1 система имеет координаты 
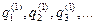, а в момент времени t2 - координаты 
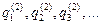, то между этими положениями система движется так, что функционал 
имеет наименьшее значение.
Функция L называется функцией Лагранжа данной системы, а интеграл S - действием. Функция Лагранжа может быть использована для характеристики не только системы с конечным числом степеней свободы, но и для сложных сред, а также для различных полей.
Этот принцип иногда называют принципом Гамильтона. Из него получаются знаменитые уравнения движения механической системы - уравнения Лагранжа:
(I.1)
где s - число степеней свободы.
Уравнения Лагранжа равнозначны уравнениям Ньютона:
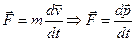(I.2)
Их отличия состоят в том, что в уравнения Ньютона входят векторные величины, а в уравнения Лагранжа - скалярные. Для системы из N частиц число уравнений Ньютона равно 3N. Уравнений Лагранжа меньше. Например, для двухатомных молекул 
. В уравнениях Ньютона не учитываются связи между частицами.
Наконец, уравнения Лагранжа могут быть записаны для любых координат, а не только декартовых.
Стоит отметить, что функция Лагранжа фактически является разностью кинетической и потенциальной энергий:
(I.3)
Для системы невзаимодействующих материальных точек с массами ma:
(I.4)
Если в системе материальных точек они взаимодействуют только друг с другом, но не взаимодействуют с какими-либо посторонними телами, то такая система называется замкнутой.
Взаимодействие между материальными точками может быть описано прибавлением к функции Лагранжа невзаимодействующих точек определённой зависящей от характера взаимодействия функции координат:
(I.5)
Для выяснения свойств функции Лагранжа надо вспомнить определение и свойства однородных функций. Они потребуются нам для записи выражения энергии при рассмотрении закона сохранения энергии.
Поиск по сайту: