Уравнение Шредингера для атома водорода

Данное уравнение имеет следующий вид:

(II.98)

Или в сферических координатах:

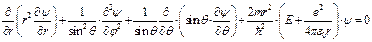(II.99)

представим волновую функцию в виде произведения радиальной и угловой частей и подставим в уравнение (II.99)

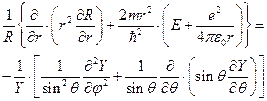(II.100)

Приравняем левую и правую часть уравнения (II.100) одной и той же величине – 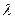. Получим два уравнения – одно для радиальной части и другое для угловой части:

(II.100 а)

(II.100 б)

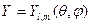полагаем, что и тогда уравнение (II.100 а) такое же, как для жесткого ротатора. Таким образом, имеем и .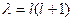

решение уравнения (II.100 б) аналогично решению уравнения для гармонического осциллятора. Энергия n-го уровня

, n=1,2,3… … (II.101)

a₀ – радиус первой боровской орбиты, a₀ = 0,529177 Å.

Сферические гармоники или угловые части 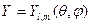выражаются, как и для жесткого ротатора через присоединенный полином Лежандра. Радиальные функции 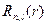выражаются через функции Лагерра 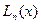. Эти функции для функции 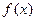имеют вид:

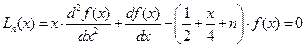(II.102)

Таким образом, мы имеем решение стационарного уравнения Шредингера для атома водорода в виде произведения угловой и радиальной частей, которые принято называть атомными орбиталями или АО. Они записываются как функции трех переменных с тремя индексами - АО.

n – главное квантовое число и оно определяет энергию электрона

l – орбитальное квантовое число и оно определяет форму атомной орбитали

m – магнитное квантовое число и оно определяет в пространстве направление атомной орбитали

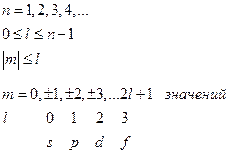(II.103)

Волновые функции атома водорода представляют собой основные структурные единицы при построении молекулярных волновых функций. При этом важны даже не сами водородные функции, а функции родственного типа для так называемых водородоподобных атомов, которые мы и рассмотрим подробнее на конкретных примерах. Но прежде определим, какие же атомы называются водородоподобными.

Водородоподобные атомы – это системы, состоящие из ядра с Z протонами и одного электрона. То есть это атомы с зарядом [(Z-1)e]⁺.

Напишем несколько функций для водородоподобных атомов в явном виде. Сначала напишем их для радиальной части для нескольких значений l и m

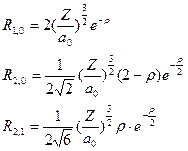, (II.104)

где 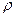– безразмерный параметр, 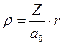, а первый и второй индексы при R обозначают l и m, соответственно.

Максимальное количество орбиталей на энергетическом уровне или кратность вырождения определяется по формуле .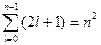

Угловые части АО выглядят следующим образом:

s – АО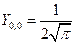

p – AO (II.105)

d – AO

Неудобством таких угловых функций является то, что среди них встречаются комплексные функции, которые нельзя изобразить в действительном пространстве. Однако из них можно получить удобные действительные функции – атомные орбитали, составляя линейные комбинации сферических гармоник с одинаковым квантовым числом l и одинаковым значением m.

Например, рассмотрим линейную комбинацию:

(II.106)

Подставим последние две формулы в выражение для p_x:

Аналогичным способом можно построить две другие атомные орбитали с l = 1, обозначения которых также понятны:

(II.107)

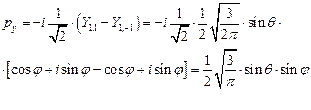(II.108)

Так же можно перейти от комплексных угловых функций для n=2 - 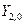, , 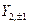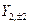к действительным АО, обозначаемым как , соответственно.

Теперь вспомним, что атомные орбитали получаются в результате перемножения угловой и радиальной частей. И выпишем несколько нормированных волновых функций водородоподобного атома:

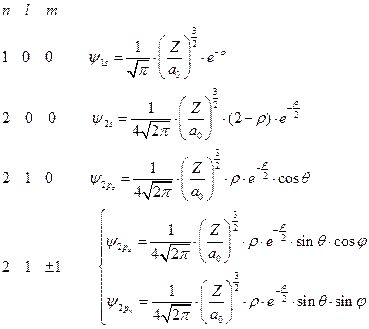
(II.109)

В химических приложениях часто используют графическое изображение волновых функций, причем, как правило, отдельно изображаются радиальная и угловая части. Выделяют только ту часть, которая зависит только от угловых переменных 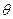и . Она имеет смысл полного выражения для АО, в котором условно принимают, что АО является произведением некоторой радиальной функции и определенной функции, зависящей от углов 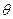и . Например, для 2pz атомной орбитали эта функция имеет следующий вид: 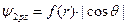. Ее в учебниках химии изображают в виде гантели, вытянутой вдоль оси Оz, как это показано на Рис. 6 а. На Рис.6 б и в показаны 2py и 2px атомные орбитали.

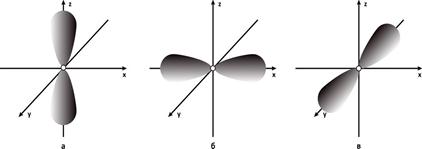
Рис.6. Электронные облака p – орбиталей: а - 2p_z- АО, б - 2p_y- АО, в - 2p_x- АО.

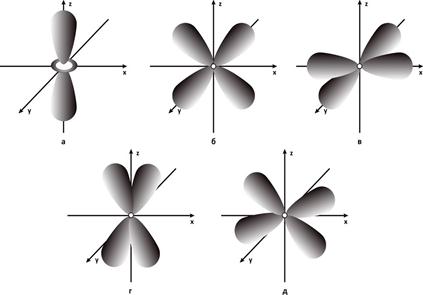
Рис.7. Электронные облака d – орбиталей: а - 3dz^2-АО; б - 3dxz-АО; в - 3dx²-y²-АО; г - 3dyz-АО; д - 3dxy-АО_.

На Рис. 7 приведено схематическое изображение d- АО, точнее их угловых частей. АО с главным квантовым числом 3 называются f – орбиталями. Они выглядят еще сложнее и изображать их графически достаточно трудно.

Здесь необходимо сделать одно важное замечание – широко используемые в химии атомные орбитали: s, p, d и т.д. являются, прежде всего, решениями стационарного уравнения Шредингера для атома водорода и водородоподобных атомов. И, наверное, благодаря тому, что атомы в значительной мере сохраняют свои свойства при образовании молекул, атомные орбитали явились очень плодотворной математической моделью, имеющей глубокое физическое значение при описании физико-химических свойств множества молекул. Не стоит забывать также и то, что, изображенные на Рис. 6 и 7 электронные облака, прежде всего, означают вероятность распределения в пространстве электронной плотности.

Поиск по сайту: