Уравнения Хартри-Фока

В приближении Хартри – Фока по отношению к полной энергии оптимизируется не просто произведение одноэлектронных волновых функций, а антисимметризованное произведение. То есть вместо волновой функции системы в виде простого произведения одноэлектронных бесспиновых функций берется детерминант Слейтера. Уравнения Хартри были получены в 1928 году и усовершенствованы Фоком в 1930 году. Они выводятся применением вариационного принципа к уравнению Шредингера для системы из N электронов. То есть в качестве пробной функции 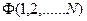берется антисимметризованное произведение спин – орбиталей, которые необходимо определить:

(III.52)

где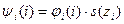

Гамильтониан системы будет ,

где

Как было показано выше, средняя энергия такой системы равна:

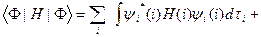
(III.53)

Варьирование производится путем варьирования всех одноэлектронных спин -орбиталей при условии

(III.54)

Умножив (Ш.54) на неопределенный множитель Лагранжа , получим для варьирования выражение:

(III.55)

Знак минус взят для удобства дальнейшей физической интерпретации. Учитывая независимость вариаций волновых функций, получается следующая система уравнений, называемая уравнениями Хартри – Фока:

Каждое из N уравнений содержит все N функций и представляет собой систему интегро – дифференциальных уравнений для нахождения N функций

Введем операторы 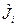и 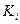определяемые равенствами:

(III.57)

(III.58)

Тогда уравнение (III.56) приобретает вид:

,

где (III.59)

Оператор 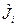допускает простую интерпретацию: это кулоновский потенциал, создаваемый в точке нахождения первого электрона распределенным в пространстве зарядом второго электрона, причем плотность этого распределения задается квадратом модуля спин – орбитали . По этой причине этот оператор называют кулоновским.

Оператор имеет более сложный характер, то есть при действии на функцию он переводит её в функцию 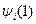. Причем знак потенциала, определяемого этим оператором, может быть не только положительным в отличие от потенциала, определяемого кулоновским оператором, который всюду положителен. Это связано с антисимметричностью волновой функции, то есть с перестановками индексов (обменом) электронов в (III.58). Поэтому такой оператор называют обменным.

Оператор эрмитов и инвариантен по отношению к унитарному преобразованию спин – орбиталей . С другой стороны, так как , то составляют эрмитову матрицу, которую можно с помощью унитарного преобразования привести к диагональному виду.

при . (III.60)

или кратко эти уравнения можно записать так:

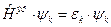(III.61)

Так же, как и система уравнений Хартри, система уравнений Хартри-Фока может быть решена с помощью метода последовательных итераций, вплоть до самосогласования.

Оператор часто записывают так:

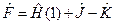(III.62)

Оператор эрмитов, который называют фокианом или оператором Фока, и одинаков для всех N уравнений, так что система уравнений фактически представляет собой одно уравнение:

, (III.63)

которому должны удовлетворять все спин -орбитали . Это уравнение имеет бесконечно много решений. Принадлежащие N низшим значениям орбитальной энергии , спин -орбитали , называют занятыми спин -орбиталями. Построенное из них антисимметризованное произведение, является, согласно вариационному принципу, наилучшим для данных пробных спин- орбиталей приближением к волновой функции основного состояния системы. Решения принадлежащие более высоко лежащим значениям орбитальной энергии 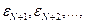называют виртуальными спин-орбиталями. Совокупность “собственных решений” () эрмитова оператора отличается тем, что орбитальные энергии действительны, а спин -орбитали, принадлежащие различным орбитальным энергиям, взаимно ортогональны. Занятые и виртуальные спин -орбитали образуют полную ортонормированную систему функций.

Поскольку в гамильтониане мы пренебрегали спин-орбитальным взаимодействием, одноэлектронные функции имеют вид , где функция S равна a или b, причем .

Поиск по сайту: