АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Элементы комбинаторики

Читайте также:
  1. I. МЕХАНИКА И ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
  2. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  3. Атрибуты (элементы данных).
  4. Банковская система и ее элементы взаимосвязи
  5. В суперсистеме всегда найдутся те элементы, которые необходимы для развития
  6. В чем проявляются элементы государственности в праве Европейского Союза?
  7. Виды и основные элементы премиальных систем
  8. ВИТАМИНЫ, МИКРОЭЛЕМЕНТЫ, АНАБОЛИКИ
  9. ВНУТРЕННЯЯ СРЕДА ОРГАНИЗАЦИИ И ЕЕ ЭЛЕМЕНТЫ
  10. Внутренняя среда: элементы и характеристики.
  11. Возможные составляющие элементы предоперационной подготовки.
  12. Вопрос 16. Автомобильная дорога, основные элементы автомобильной дороги.

Элементарная (но необязательно простая) часть теории вероятностей опирается на комбинаторику. Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Приведем некоторые сведения.

Пусть имеется конечное число различных объектов произвольной природы, которые назовем элементами. Из них по определенному правилу можно образовать некоторые группы.

Перестановками называются группы, состоящие из элементов и отличающиеся друг от друга только порядком их следования.

Число возможных перестановок из элементов вычисляется по формуле:

. (4.1)

Пример 4.1. Даны цифры 1, 2, 3, 4, 5. Сколько различных пятизначных чисел можно их них составить?

Решение. Применяем формулу (4.1). !=120.

Размещениями по m элементов из n называются группы, состоящие из m элементов и отличающиеся друг от друга порядком их следования и составом.

Число возможных размещений вычисляется по формуле:

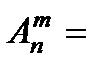
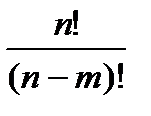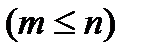, (4.2)

Пример 4.2. Даны цифры 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно их них составить?

Решение. Применяем формулу (4.2).

Сочетаниями по m элементов из n называются группы, состоящие из m элементов и отличающиеся друг от друга только составом.

Число возможных сочетаний вычисляется по формуле:

. (4.3)

Некоторые свойства сочетаний:

1º. .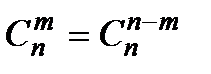

2º. .

 

Пример 4.3. В колоде 36 карт, сдаем по 6 (играем в «дурака»). Сколько различных наборов карт может быть?

Решение. Так как в этой игре порядок прихода карт при раздаче не важен, применяем формулу (4.3).

.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)