АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формула (1.4) представляет собой правило составления элементов матрицы C,

Читайте также:
  1. IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.
  2. SWOT- анализ и составление матрицы.
  3. VII. Идея и деление особой науки, называемой критикой чистого разума
  4. Алгоритмы упорядочивания элементов в массивах
  5. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  6. Барометрическая формула
  7. Барометрическая формула. Распределение Больцмана.
  8. Биогеохимические круговороты основных химических элементов в биосфере
  9. Бухгалтерский баланс и порядок его составления
  10. Быть собой
  11. В 72-х дневном цикле подвиг длится 8 суток, из которых 2 суток – голод, а 6 – очистительные процедуры и работа над собой. В 12-ти летнем цикле подвиг длится 1 год.
  12. В зависимости от наличия тех или иных морфологических элементов сыпи выделяют различные типы дермального ангиита.

являющейся произведением матрицы A на матрицу B. Это правило можно сформулировать и словесно: Элемент Cij, стоящий на пересечении i-й строки и j-го столбца матрицы C = AB, равен сумме попарных произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы B. В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц второго порядка

=

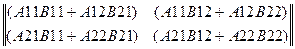
Из формулы (1.4) вытекают следующие свойства произведения матрицы A на матрицу B:

1) сочетательное свойство: (AB) C = A (BC);

2) распределительное относительно суммы матриц свойство:

(A + B) C = AC + BC или A (B + C) = AB + AC.

Вопрос о перестановочном свойстве произведения матриц имеет смысл ставить лишь для квадратных матриц одинакового порядка. Элементарные примеры показывают, что произведений двух квадратных матриц одинакового порядка не обладает, вообще говоря, перестановочным свойством. В самом деле, если положить

A = , B = , то AB = , а BA =


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |

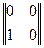
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)