АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема: Парная линейная регрессия и корреляция. 1. Расчет параметров парной регрессии по методу наименьших квадратов

Читайте также:
  1. Банковская система: понятие, типы, структура. Формирование и развитие банковской системы России
  2. Вывод: график зависимости совместного изменения двух изучаемых параметров показывает наличие взаимосвязи, которая приближенно оценивается как линейная.
  3. Денежная система: понятие, элементы, типы. Особенности денежной системы РФ
  4. Економічна система: сутність, структурні елементи і критерії класифікації.
  5. Задача Д1 (тема: “Динамика точки”)
  6. Задачи 6-12 Линейная алгебра
  7. Занятие 13. Тема: «Новая драма». С. Беккет «В ожидании Годо».
  8. Змішана” соціально-економічна система: закономірності формування, елементи, моделі
  9. Кредитна система: суть, види, ознаки, складові
  10. Кредитная система: сущность и устройство
  11. Линейная зависимость векторов
  12. Линейная зависимость и независимость векторов

Содержание занятия.

1. Расчет параметров парной регрессии по методу наименьших квадратов.

2. Расчет линейного коэффициента корреляции и коэффициента детерминации.

Литература: [1] стр41-48, [3] стр55-64, [5] стр141-147, [11] стр3-6

 

Задание Имеются следующие исходные данные:

Предприятие Выпуск продукции, тыс.ед., х Затраты на производство, млн. тенге, у
     

Определить параметры парной линейной регрессии. Рассчитать значение линейного коэффициента корреляции и коэффициента детерминации. Сделать выводы.

 

Методические указания по выполнению задания:

1. Для определения параметров парной линейной регрессии необходимо провести следующие расчеты:

№ x y yx
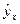
            31,09 141,84 104,92 68,01 104,92 178,76 215,67 141,84 104,92 68,01
Итого            
среднее 3,3     12,9   -

Рассчитаем параметры a и b: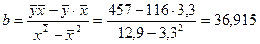

Уравнение регрессии имеет следующий вид:

Охарактеризуем результаты построенного уравнения регрессии: с увеличением выпуска продукции (х) на 1 тыс. единиц затраты на производство возрастут в среднем на 36,915 млн.тенге.

Подставив в уравнение регрессии значения фактора х, найдем теоретические значения 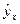(7 графа таблицы)

 

2. Уравнение регрессии дополняется показателем тесноты связи - линейным коэффициентом корреляции:

Данный линейный коэффициент корреляции означает о наличии тесной зависимости затрат на производство от величины объема выпущенной продукции.

Определим коэффициент детерминации: . Вариация результата на 99,1% объясняется вариацией фактора х, а на долю прочих неучтенных факторов в данной регрессионной модели приходится лишь 0,9%.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)