АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема: Модель множественной линейной регрессии. 1.Оценка параметров уравнения множественной регрессии методом наименьших квадратов

Читайте также:
  1. XXII. Модель «К» и отчаянный риск
  2. А) Модель Хофстида
  3. Адаптивная модель
  4. Адаптивная полиномиальная модель первого порядка
  5. Альтернативні моделі розвитку. Центральна проблема (ринок і КАС). Азіатські моделі. Європейська модель. Американська модель
  6. Анализ финансовой устойчивости. Модель финансовой устойчивости
  7. Англо-американская модель, оплата труда руководства верхнего уровня
  8. Арифметические выражения и алгоритм линейной структуры
  9. Базовая модель структурного построения производственных систем
  10. Базовая модель управления персоналом
  11. Банковская система: понятие, типы, структура. Формирование и развитие банковской системы России
  12. Белорусская модель социально ориентированной рыночной экономики – элемент идеологии белорусского государства

Содержание занятия:

1.Оценка параметров уравнения множественной регрессии методом наименьших квадратов.

2. Построение уравнения множественной линейной регрессии в стандартизованном масштабе.

Литература: [1] стр105-109, 112-120, [4] стр81-84

Задание Изучается зависимость выработки продукции на одного работника у (тыс. д.ед.) от ввода в действие новых основных фондов х1 (% стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).

Номер предприятия у х1 х2
    3,9 3,9 3,7 4,0 3,8 4,8 5,4 4,4 5,3 6,8 6,0 6,4 6,8 7,2 8,0 8,2 8,1 8,5 9,6 9,0  
средние 9,6 6,19 22,3

1.Определить параметры уравнения множественной регрессии по методу наименьших квадратов.

2. Построить уравнения множественной регрессии в стандартизованном масштабе.

 

Методические указания по выполнению задания:

Для определения параметров множественной линейной регрессии следует воспользоваться ППП MS Excel Анализ данных. Для этого:

1) в главном меню выберите пункты Сервис/ Анализ данных/ Регрессия. Щелкните по кнопке ОК.

2) заполните диалоговое окно ввода данных и параметров вывода:

входной интервал Y - диапазон, содержащий данные результативного признака;

входной интервал Х - диапазон, содержащий данные факторов независимого признака. Щелкните по кнопке ОК.

По результатам вычислений получено уравнение множественной регрессии вида:

Коэффициент «чистой» регрессии при параметре х1 показывает, что при увеличении ввода в действие основных фондов на 1% выработка продукции на одного работника увеличивается на 0,9459 тыс. д. ед. при устранении влияния действия удельного веса рабочих высокой квалификации в общей численности рабочих. Аналогично интерпретируется показатель «чистой» регрессии при параметре х2. С увеличением удельного веса рабочих высокой квалификации в общей численности рабочих на 1% выработка продукции на одного работника увеличивается на 0,0856 тыс.д.ед. при устранении влияния основных фондов.

Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя, инструмент анализа данных Корреляция. Для этого:

1) в главном меню последовательно выберите пункты Сервис/ Анализ данных/ Корреляция. Щелкните по кнопке ОК

2) заполните диалоговое окно ввода данных и параметров вывода.

3) результаты вычислений – матрица коэффициентов парной корреляции.

  Столбец 1 Столбец 2 Столбец 3
Столбец 1      
Столбец 2 ryx1    
Столбец 3 ryx2 rx1x2  

Результаты вычислений данной задачи: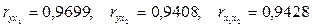

Значения коэффициентов парной корреляции указывают на очень тесную связь выработки у как с коэффициентом обновления основных фондов - х1, так и с долей рабочих высокой квалификации - х2. Но в то же время межфакторная связь весьма тесная и превышает тесноту связи х2 с у. В связи с этим для улучшения данной можно исключить из нее фактор х2 как недостаточно статистически надежный.

Расчет стандартизованных переменных следует выполнить по формулам:

 

Уравнение регрессии в стандартизованном масштабе имеет вид:

С увеличением основных фондов на 1 (сигму) выработка продукции на одного работника увеличивается на 0,7461 при устранении влияния действия удельного веса рабочих высокой квалификации в общей численности рабочих. С увеличением удельного веса рабочих высокой квалификации в общей численности рабочих на 1 выработка продукции на одного работника увеличивается на 0,2374 при устранении влияния основных фондов. Сравнивая стандартизованные коэффициенты регрессии можно сделать вывод, что наибольшее влияние на результативный признак оказывает влияние фактор х1.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)