Тема: Система одновременных уравнений. 1. Применение косвенного метода наименьших квадратов

Содержание занятия.

1. Применение косвенного метода наименьших квадратов.

2. Применение ДМНК к простейшей сверхидентифицируемой модели.

Литература: [1] стр200-204,[2] стр113-115, [8] стр30-341

Задание

Пусть для построения данной модели мы располагаем некоторой информацией по 5 регионам:

Построить структурную эконометрическую модель, применив косвенный метод наименьших квадратов и двухшаговый метод наименьших квадратов.

Методические указания по выполнению задания: Приведенная форма модели составит:

Для каждого уравнения приведенной формы модели применяем традиционный МНК и определяем 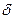-коэффициенты. Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т.е. 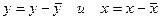. Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:

№
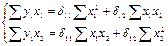
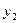
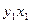
	-2 -1	-1,2 -0,2 0,8 1,8 -1,2	-1,4 -0,4 0,6 -0,4 1,6	-0,4 -2,4 -1,4 1,6 2,6	2,8 0,4 -0,4 3,2	0,8 2,4 1,6 5,2	1,96 0,16 0,36 0,16 2,56	0,16 5,76 1,96 2,56 6,76	0,56 0,96 -0,84 -0,64 4,16	1,68 0,08 0,48 -0,72 -1,92	0,48 0,48 -1,12 2,88 -3,12
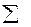
							5,2	17,2	4,2	-0,4	-0,4

Применительно к рассматриваемому примеру, используя отклонения от средних уровней, имеем: . Решая данную систему, получим следующее первое уравнение приведенной формы модели:

у₁=0,852х₁+0,373х₂ Аналогично применяем МНК для второго уравнения приведенной формы модели. Система нормальных уравнений составит: Применительно к нашему примеру имеем:

Откуда второе уравнение приведенное уравнение составит: у₂=-0,072х₁-0,00557х₂

Таким образом, приведенная форма модели имеет вид:

Переходим от приведенной формы к структурной форме модели, т.е. к системе уравнений:

Для этой цели из первого уравнения приведенной формы модели надо исключить х₂ выразив его из второго уравнения приведенной формы и подставив в первое: . Тогда

- первое уравнение структурной модели.

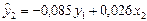Чтобы найти второе уравнение структурной модели обратимся вновь к приведенной форме модели. Из второго уравнения приведенной формы модели следует исключить х₁, выразив его через первое уравнение и подставив во второе: и . - второе уравнение структурной модели.

Итак, структурная форма модели имеет вид:

Применим двухшаговый метод наименьших квадратов к простейшей сверхидентифицируемой модели: . Используем те же исходные данные, поэтому получим ту же систему приведенных уравнений:

На основе второго уравнения данной системы найдем теоретические значения для эндогенной переменной 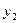, т.е. . С это целью во второе уравнение подставляем значения и .

Расчетные данные для второго шага ДМНК.

			+ = z
-1,4 -0,4 0,6 -0,4 1,6	-0,4 -2,4 -1,4 1,6 2,6	0,103 0,042 -0,035 0,020 -0,130	-1,297 -0,358 0,565 -0,380 1,470	-2 -1	2,594 0,358 -0,380 2,940	1,682 0,128 0,319 0,144 2,161
					5,512	4,434

Заменяя фактические значения 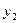их оценками , найдем значения новой переменной + = z. Далее применяем МНК к уравнению е.е. 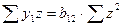. Откуда .

Таким образом, сверхидентифицируемое структурное уравнение составит 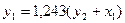. Ввиду того, что второе уравнение системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений та же: . В целом рассматриваемая система одновременных уравнений составит:

8. Материалы для самостоятельной работы обучающегося:

Поиск по сайту: