 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Электромагнитные волны. Систему уравнений Максвелла, записанную для однородной непроводящей среды, где и , можно свести к двум дифференциальным уравнениям второго порядка с
Систему уравнений Максвелла, записанную для однородной непроводящей среды, где  и
и  , можно свести к двум дифференциальным уравнениям второго порядка с постоянными коэффициентами
, можно свести к двум дифференциальным уравнениям второго порядка с постоянными коэффициентами
 (62.1)
(62.1)
 (62.2)
(62.2)
которые являются волновыми уравнениями двух плоских гармонических волн, представляющих собой синхронное (с одинаковой фазой) однонаправленное распространение в среде колебаний векторов  и
и 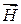 :
:
 (62.3)
(62.3)
 (62.4)
(62.4)
(формулы (62.3) и (62.4) записаны для частного случая распространения колебаний вдоль оси x).
Следовательно, электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов — и распространяться в среде в виде электромагнитных волн со скоростью
 (62.5)
(62.5)
где  — скорость электромагнитных волн в вакууме.
— скорость электромагнитных волн в вакууме.
 Рис.62.1
Рис.62.1
| Векторы  и и 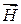 взаимно перпендикулярны и образуют с направлением распространения волны (вектором скорости волны) правовинтовую систему (рис. 62.1).
Из синхронности колебаний векторов взаимно перпендикулярны и образуют с направлением распространения волны (вектором скорости волны) правовинтовую систему (рис. 62.1).
Из синхронности колебаний векторов  и и 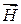 и вытекает соотношение и вытекает соотношение
 (62.6) (62.6)
|
где E и H — модули векторов  и
и 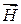 .
.
Электромагнитные волны переносят энергию. Объемная плотность энергии электромагнитного поля (см. формулы (42.5) и (58.5))
 (62.7)
(62.7)
С учетом соотношения (62.6) перепишем выражение (62.7) в виде
 (62.8)
(62.8)
(мы учли формулу (62.5)).
Умножим объемную плотность w энергии электромагнитного поля на скорость v электромагнитной волны и обозначим это произведение буквой S:
 (62.9)
(62.9)
Произведение wv имеет размерность  — размерность плотности потока электромагнитной энергии, по определению равной электромагнитной энергии, переносимой электромагнитной волной за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны.
— размерность плотности потока электромагнитной энергии, по определению равной электромагнитной энергии, переносимой электромагнитной волной за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны.
Назовем вектор  вектором Пойнтинга, модуль которого равен плотности потока электромагнитной энергии, а направление совпадает с направлением распространения электромагнитной волны.
вектором Пойнтинга, модуль которого равен плотности потока электромагнитной энергии, а направление совпадает с направлением распространения электромагнитной волны.
Так как векторное произведение векторов  и
и 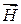

также совпадает с направлением распространения электромагнитной волны (см. рис. 62.1), то с учетом выражения (62.8) можем написать
 (62.10)
(62.10)
Поиск по сайту: