I. Решение логических задач средствами алгебры логики

Обычно используется следующая схема решения:

1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
4. определяются значения истинности этой логической формулы;
5. из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.

Пример 1. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.

— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.

— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.

Питер, к которому обратился Ник, возмутился:

— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.

По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?

Решение. Введем обозначения для логических высказываний:

Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.

Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.

Зафиксируем высказывания каждого из друзей:

Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание

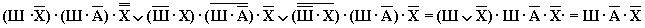
Высказывание 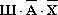истинно только при Ш=1, А=0, Х=0.

Ответ. Победителем этапа гонок стал Шумахер.

Пример 2. Некий любитель приключений отправился в кругосветное путешествие на яхте, оснащённой бортовым компьютером. Его предупредили, что чаще всего выходят из строя три узла компьютера — a, b, c, и дали необходимые детали для замены. Выяснить, какой именно узел надо заменить, он может по сигнальным лампочкам на контрольной панели. Лампочек тоже ровно три: x, y и z.

Инструкция по выявлению неисправных узлов такова:

1. если неисправен хотя бы один из узлов компьютера, то горит по крайней мере одна из лампочек x, y, z;
2. если неисправен узел a, но исправен узел с, то загорается лампочка y;
3. если неисправен узел с, но исправен узел b, загорается лампочка y, но не загорается лампочка x;
4. если неисправен узел b, но исправен узел c, то загораются лампочки x и y или не загорается лампочка x;
5. если горит лампочка х и при этом либо неисправен узел а, либо все три узла a, b, c исправны, то горит и лампочка y.

В пути компьютер сломался. На контрольной панели загорелась лампочка x. Тщательно изучив инструкцию, путешественник починил компьютер. Но с этого момента и до конца плавания его не оставляла тревога. Он понял, что инструкция несовершенна, и есть случаи, когда она ему не поможет.

Какие узлы заменил путешественник? Какие изъяны он обнаружил в инструкции?

Решение. Введем обозначения для логических высказываний:

a — неисправен узел а; x — горит лампочка х;

b — неисправен узел b; y — горит лампочка y;

с — неисправен узел с; z — горит лампочка z.

Правила 1–5 выражаются следующими формулами:

Формулы 1–5 истинны по условию, следовательно, их конъюнкция тоже истинна:

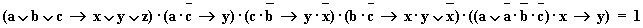
Выражая импликацию через дизъюнкцию и отрицание (напомним, что ), получаем:

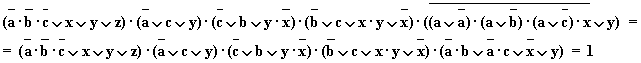
Подставляя в это тождество конкретные значения истинности x =1, y =0, z =0, получаем:

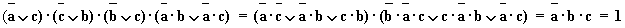
Отсюда следует, что a=0, b=1, c=1.

Ответ на первый вопрос задачи: нужно заменить блоки b и c; блок а не требует замены. Ответ на второй вопрос задачи получите самостоятельно.

Поиск по сайту: