Сложение колебаний, направленных вдоль одной прямой

Возможны случаи, когда на тело действуют несколько упругих сил. Каждая из этих сил заставляет тело совершать гармоническое колебание. При одновременном воздействии этих сил тело одновременно будет участвовать во всех этих движениях. Примером может служить барабанная перепонка, одновременно воспринимающая множество звуковых колебаний. В этом случае, чтобы найти результирующее движение, необходимо сложить колебания.

Рассмотрим случай, когда тело одновременно участвует в двух колебаниях с одинаковыми частотами, но разными амплитудами и начальными фазами:

,

.

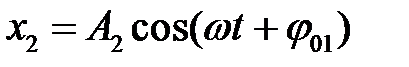Результирующее колебание также является гармоническим и определится суммой смещений

.

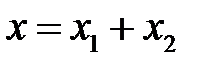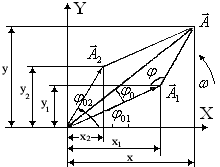Рисунок 3.4

Для определения результирующего смещения применяется векторный метод сложения колебаний (см. рисунок 4), так как любое гармоническое колебание можно описать с помощью радиус – вектора, модуль которого равен амплитуде колебания (см. раздел 3.1).

Углы отсчитывается от положительного направления оси О Х. На рисунке 3.4 изображены положения векторов 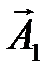и в начальный момент , т.к векторы вращаются с одинаковой угловой скоростью, то и их результирующий вектор будет вращаться с той же угловой скоростью, т.е., результирующее движение также будет гармоническим с круговой частотой :

.

Амплитуду этого колебания можно найти по теореме косинусов:

,

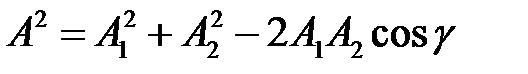, поэтому

. (3.13)

Начальную фазу результирующего колебания можно определить из начальных условий:

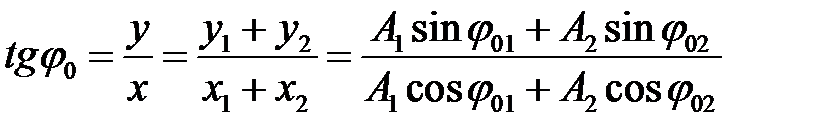. (3.14)

Анализируя уравнение (3.13), видим, что при сложении одинаково направленных колебаний возможны следующие случаи:

1) если разность фаз равна четному числу p, т.е.

,

где 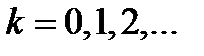(можно считать, что ), то колебания совпадают по фазе и усиливают друг друга. В этом случае

Рисунок 3.5

,

,

т.е. результирующая амплитуда равна сумме амплитуд составляющих колебаний (см. рисунок 3.5).

2) При разности фаз, равной нечетному числу p

, ,

,

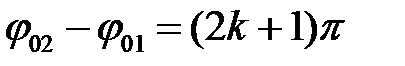, (3.15)

Рисунок 3. 6

т.е. колебания ослабляют друг друга и результирующая амплитуда равна разности амплитуд складываемых колебаний (см. рисунок 3.6). При , т.е., если амплитуды складываемых колебаний одинаковы и колебания совершаются в противофазе, то колебания друг друга гасят.

3) Если складываемые колебания имеют одинаковые амплитуды (), но частоты складываемых колебаний не одинаковы, то результирующее колебание не будет гармоническим.

Рисунок 3.7

Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте . Результирующее колебание при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой (см. рисунок 3.7). Такие колебания называются биениями. График изменения амплитуды со временем показан на рисунке 3.7б.

3.6. Затухающие колебания

В реальных условиях на тело со стороны окружающей среды действуют силы трения, препятствующие движению. На преодоление сил трения расходуется энергия. Поэтому энергия колеблющегося тела уменьшается и, следовательно, уменьшается амплитуда колебаний, т.е., колебания становятся затухающими (см. уравнение (3.12)).

Запишем второй закон Ньютона для реальных условий:

,

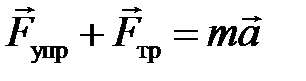поскольку все силы действуют вдоль одной линии, то в скалярном виде уравнение движения будет иметь вид: .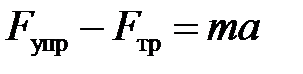

При небольших скоростях движения сила трения пропорциональна скорости и направлена противоположно ей, поэтому

,

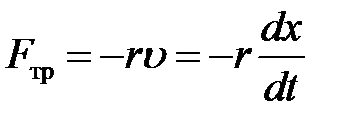где µ – коэффициент трения. Тогда второй закон Ньютона запишется:

перенесем все члены уравнения в левую часть и разделим на m:

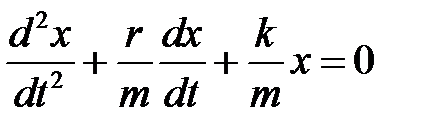. (3.16)

Получили дифференциальное уравнение затухающих колебаний, общее решение которого будет иметь следующий вид:

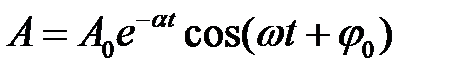, (3.17)

где 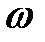– круговая частота затухающих колебаний:

. (3.18)

Выражение (3.17) является уравнением затухающих колебаний. Оно отличается от чисто гармонического колебания тем, что амплитуда колебания с течением времени уменьшается (см. рисунок 3.8). Пунктиром на этом рисунке изображена зависимость амплитуды от времени.

Рисунок 3.8

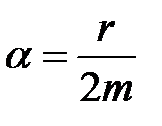– называют коэффициентом затухания, чем больше коэффициент затухания , тем быстрее затухают колебания. На практике степень затухания характеризуется логарифмическим декрементом затухания. Логарифмический декремент затухания 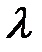– это натуральный логарифм отношения двух амплитуд затухающего колебания, отличающихся на один период:

.

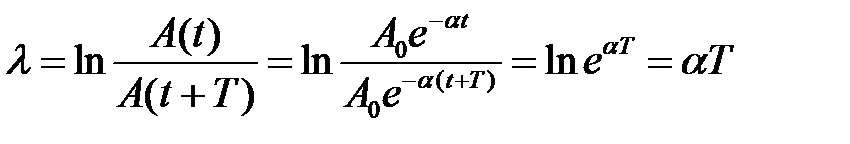Физический смысл логарифмического декремента затухания заключается в том, что это величина, обратная числу колебаний, после которых амплитуда уменьшается в 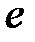раз:

,

где – число колебаний, которое успевает совершить колеблющееся тело за время, в течение которого амплитуда колебаний уменьшается в е раз.

С увеличением трения частота колебаний уменьшается, а период соответственно увеличивается. При равенстве коэффициента затухания частоте собственных колебаний , частота затухающих колебаний , а 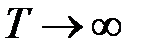, движение становится апериодическим, т.е., при большом трении выведенное из равновесия тело затем медленно возвращается к положению равновесия, колебания не возникают.

Поиск по сайту: