Электростатика. Электростатика изучает свойства и закономерности систем неподвижных электрических зарядов и процессы

Электростатика изучает свойства и закономерности систем неподвижных электрических зарядов и процессы, происходящие в телах, помещенных в электрическое поле. Имеется бесчисленное множество практических применений теории электричества. Электрические силы определяют строение атомов и молекул. Электричество связано со многими биологическими процессами, например, с действием наших нервов и мозга.

5.1 Основные закономерности электростатики

В основе электростатики лежат следующие закономерности:

1) фундаментальным свойством электрического заряда является его существование в двух видах. Заряды бывают положительными и отрицательными; названия условны и подчеркивают лишь то, что одноименные заряды отталкиваются, а разноименные притягиваются;

2) полный заряд изолированной системы представляет собой величину, которая никогда не изменяется, т.е. 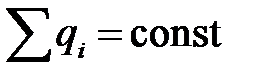. Под изолированной мы понимаем такую систему, через границы которой не может проникнуть никакое другое вещество;

3) всякий заряд образуется совокупностью элементарных зарядов, поэтому он является целым кратным заряду электрона 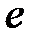=1,6×10^-19 Кл: , где целое отрицательное или положительное число. Если физическая величина может принимать только определенные дискретные значения, то говорят, что эта величина квантуется;

4) величина заряда, измеряемая в различных инерциальных системах отсчета, оказывается одинаковой. Отсюда вытекает, что величина заряда не зависит от того, движется этот заряд или покоится.

5.2 Закон Кулона

Закон, которому подчиняется сила взаимодействия точечных зарядов, был установлен экспериментально в 1785г. Кулоном. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.

В результате своих опытов Кулон пришел к выводу, что сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого заряда и обратно пропорциональна квадрату расстояния между ними, это утверждение может быть выражено формулой:

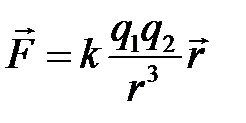, (5.1)

где и – величины, взаимодействующих зарядов, 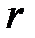– расстояние между зарядами, – коэффициент пропорциональности, который в системе СИ определяется следующим образом:

,

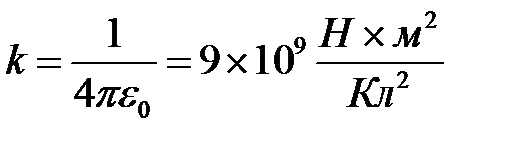где 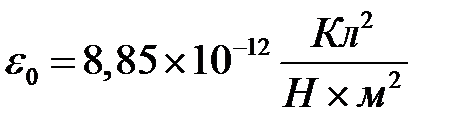и называется диэлектрической проницаемостью вакуума. На рисунке 5.1 изображены силы взаимодействия одноименных зарядов и .

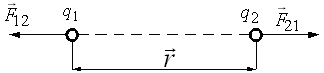Рисунок 5.1

Силы 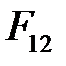и равны по величине, противоположны по направлению (3-й закон Ньютона). Значение каждой из этих сил определяются выражением (5.1).

Сила взаимодействия зависит также от среды, в которой находятся заряды. Среда ослабляет силу взаимодействия:

,

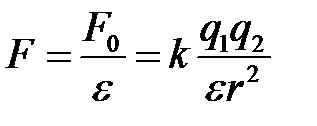где 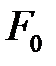– сила взаимодействия между зарядами в вакууме, – относительная диэлектрическая проницаемость среды – физическая величина, численно равная отношению силы, действующей между зарядами в вакууме к силе, действующей между зарядами в среде при прочих равных условиях .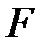

5.3 Электростатическое поле. Напряженность поля

Всякий заряд изменяет свойства окружающего его пространства, создает в нем электрическое поле. Для исследования этого поля можно использовать другие заряды, называемые в этом случае пробными.

Если в данную точку пространства вносить разные по величине пробные заряды, то и силы, действующие на них, будут разными. Но отношение силы к величине пробного заряда будет величиной постоянной для данной точки поля. Эта величина называется напряженностью электрического поля, это силовая характеристика поля.

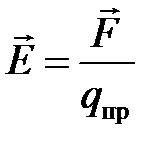. (5.2)

Напряженность численно равна силе, действующей на единичный, положительный – заряд, помещенный в данную точку поля. Определение напряженности поля показывает, что направление вектора напряженности электростатического поля совпадает с направлением силы, действующей на положительный заряд. Размерность напряженности в системе СИ:

.

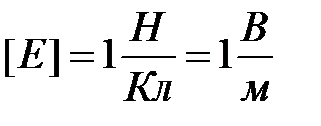В соответствии с формулами (5.1) и (5.2) следует, что напряженность поля точечного заряда пропорциональна величине заряда и обратно пропорциональна квадрату расстояния 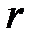от заряда до данной точки поля:

, (5.3)

где – единичный вектор, показывающий направление вектора напряженности. Из уравнения (5.3) следует, что вектор направлен вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.

Сила, действующая на пробный заряд со стороны электростатического поля равна , и на любой заряд, находящийся в электрическом поле с напряженностью 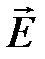будет действовать сила .

Если электростатическое поле создается не одним, а несколькими зарядами, то каждый заряд создает свое собственное поле независимо от присутствия других зарядов. Поэтому поле системы зарядов будет действовать на пробный заряд с результирующей силой, равной равнодействующей всех сил, действующих от каждого заряда в отдельности

. (5.4)

Напряженность поля, созданного несколькими зарядами, равна геометрической сумме векторов напряженности полей, созданных каждым зарядом в отдельности.

Рисунок 5.2

Это принцип суперпозиции и независимости полей. На рисунке 5.2 представлен случай суперпозиции полей, созданных двумя положительными зарядами.

Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Разбив протяженные заряды на достаточно малые доли , любую систему зарядов можно свести к совокупности точечных зарядов. Вклад каждого из таких зарядов в результирующее поле вычисляется по формуле (5.3).

Рисунок 5.3

Электрическое поле можно изображать с помощью силовых линий – это линии, касательная к которым в любой точке поля совпадает по направлению с вектором напряженности (см. рисунок 5.3). Густота силовых линий выбирается так, чтобы число силовых линий, пронизывающих единицу поверхности площадки, перпендикулярной к силовым линиям, равнялось значению вектора напряженности , т.е., по картине силовых линий можно судить о направление и величине вектора в разных точках пространства (см. рисунок 5.3).

Силовые линии электростатического поля точечного заряда (положительного и отрицательного изображены на рисунке 5.4). Также на рисунке 5.4 изображены силовые линии поля, созданного двумя зарядами.

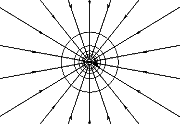
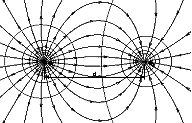
Рисунок 5.4

Таким образом, силовые линии электростатических полей могут начинаться или заканчиваться на зарядах либо уходить в бесконечность. Электростатические поля бывают однородные и неоднородные. Однородными называются поля, вектор напряженности которых во всех точках поля одинаков по величине и направлению. Такие поля изображаются параллельными силовыми линиями.

5.4 Электрические диполи

Электростатическое поле может быть создано не только зарядами, но и электронейтральными системами (суммарный заряд в такой системе равен нулю), если в этой системе пространственно разнесены центры тяжести положительных и отрицательных зарядов, примером может служить поле диполя. Электрическим диполем называется система двух одинаковых по величине, но разных по знаку точечных зарядов и , находящихся на расстоянии друг от друга (см. рисунок 5.5). Основной характеристикой диполя является дипольный момент .

Рисунок 5.5

Вектор дипольного момента направлен по оси диполя от отрицательного заряда к положительному заряду. Используя принцип суперпозиции электростатических полей, можно получить выражение для расчета напряженности поля, созданного диполем.

Рисунок 5.6

Используя рисунок 5.6 можно получить следующее выражение для модуля вектора напряженности в исследуемой точке поля

.

Из формулы видно, что напряженность электростатического поля диполя убывает с расстоянием быстрее, чем для точечного заряда (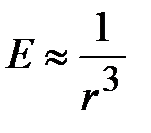 – для диполя и 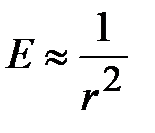для точечного заряда). Этого и следовало ожидать, так как на больших расстояниях два заряда противоположного знака оказываются столь близкими, что нейтрализуют друг друга.

Поиск по сайту: