Электромагнетизм. 7.1 Источники магнитного поля

7.1 Источники магнитного поля. Силовые линии

Постоянные магниты и проводники с током изменяют свойства окружающего его пространства, т.е. служат источниками магнитного поля. Для обнаружения и исследования этого поля можно использовать стрелку компаса, которая представляет собой постоянный магнит с точкой опоры в своем центре масс, так что он может свободно вращаться. Обращенный на север полюс свободно висящего магнита называют северным полюсом магнита (N). Противоположный полюс направлен на юг и называется южным полюсом (S).

Силу, с которой магнит (проводник с током) действует на магнитную стрелку, можно рассматривать как результат действия магнитного поля магнита (поля проводника с током) на другой магнит. Направление магнитного поля можно определить как направление, которое указывает северный полюс стрелки компаса, помещенный в эту точку поля. Магнитное поле также как и электростатическое поле можно изображать с помощью силовых линий. Силовые линии магнитного поля проводят таким образом, чтобы стрелка компаса располагалась по касательной к силовой линии магнитного поля в любой точке поля. На рисунке 7.1 показано, как с помощью стрелки компас можно установить направление одной из силовых линий магнитного поля магнитного стрежня.

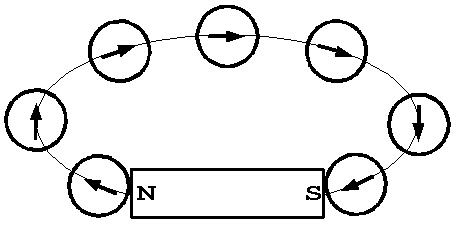Рисунок 7.1

На рисунке 7.2, также как и на рисунке 7.1 построены силовые линии для подковообразного магнита (см.рис.7.2а) и магнитного стержня (см.рис.7.2б). Обратите внимание на то, что в соответствии с нашим определением силовые линии всегда выходят из северного полюса магнита, входят в южный полюс и замыкаются внутри магнита.

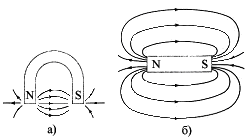Рисунок 7.2

Рассмотрим также магнитное поле, созданное проводником с током. В 1820г. Эрстед обнаружил, что магнитная стрелка, расположенная рядом с электрическим проводником, отклоняется, когда проводник подключают к источнику питания.

Вблизи прямолинейного проводника с током магнитная стрелка устанавливается по касательной к окружности, очерченной вокруг проводника с током (см. рис.7.3). Иными словами, силовые линии магнитного поля проводника с током имеют вид окружностей, в центре которых находится проводник с током (см.рис.7.4а).

Рисунок 7.3

Направление силовых линий указывается северным полюсом магнитной стрелки на рисунке 7.3. Для определения силовых линий магнитного проводника с током служит правило правой руки: проводник мысленно охватывается правой рукой так, чтобы большой палец располагался в направлении тока (положительных зарядов); тогда остальные пальцы загибаются в направлении силовых линий (см.рис.7.4б).

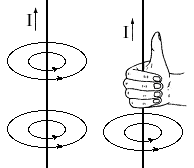а б Рисунок 7.4

7.2 Сила Ампера. Вектор индукции

магнитного поля

Рассмотрим силу, действующую на проводник с током в магнитном поле. Для этого поместим прямолинейный проводник с током между полюсами подковообразного магнита (см. рис.7.5). На проводник с током действует сила тяжести, поэтому, находясь в свободном состоянии, этот проводник должен падать.

Если в проводнике менять величину тока и направление тока, располагая проводник с током под разными углами к силовым линиям магнитного поля, то оказывается, что проводник может находиться в состоянии равновесия. Это возможно лишь в том случае, если на проводник кроме силы тяжести действует еще одна сила, направленная вертикально вверх.

Рисунок 7.5

Поскольку проводник находится в магнитном поле, то, очевидно, что эта сила действует на него со стороны магнитного поля. Из условий равновесия можно найти значение этой силы. Экспериментально обнаружено, что величина силы, действующей на проводник с током со стороны магнитного поля, прямо пропорциональна силе тока в проводнике I, длине проводника в магнитном поле l (которое предполагается однородным) и вектору магнитной индукции В (который характеризует магнитное поле). Сила зависит также от угла q между проводником и направлением силовых линий магнитного поля. Когда проводник перпендикулярен силовым линиям магнитного поля, сила максимальна; когда проводник параллелен силовым линиям, то сила обращается в нуль. В промежуточных значениях сила пропорциональна . Таким образом,

. (7.1)

Сила (7.1) получила название силы Ампера. Направление действия силы Ампера определяется правилом левой руки, которое формулируется следующим образом:

если левую руку расположить так, чтобы линии индукции входили в ладонь, а вытянутые пальцы показывали направление тока, то отогнутый большой палец покажет направление силы.

Рисунок 7.6

На рисунке 7.6 показано направление силы, действующей на проводник с током, расположенный перпендикулярно линиям индукции. Уравнение (7.1) записано для однородного поля и прямолинейного проводника. Если же поле неоднородно или проводник не везде составляет одинаковый угол с силовыми линиями, то выражение (7.1) можно записать в дифференциальной форме:

, (7.2)

где dF – сила, действующая на элемент проводника длиной dl. Полная сила, действующая на проводник, определяется интегрированием.

Из закона Ампера можно установить физический смысл вектора индукции магнитного поля

. (7.3)

Вектор индукция магнитного поля численно равен максимальной силе, действующей на прямолинейный участок проводника с током единичной длины, по которому течет ток, равный единице силы тока.

Размерность индукции в системе СИ: 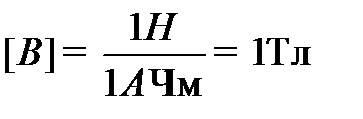(Тесла).

Магнитное поле графически изображается с помощью силовых линий, которые можно определить следующим образом: линиями магнитной индукции или силовыми линиями называются кривые, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции 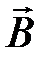в этих точках магнитного поля. Линии магнитной индукции в отличие от силовых линий электростатического поля всегда замкнуты.

Опыт показывает, что магнитные поля, создаваемые одним и тем же проводником с током в вакууме и в любой другой среде, будет различными. Это объясняется тем, что в любой среде существуют молекулярные токи, которые образованы движением электронов в атомах и молекулах. Эти молекулярные токи создают свое магнитное поле. Вектор магнитной индукции характеризует результирующее поле, создаваемое всеми молекулярными токами и проводниками с током.

Для характеристики магнитного поля, создаваемого только проводником с током, вводится вектор напряженности магнитного поля , не зависящий от свойств среды. Между векторами индукции и напряженности существует связь , m – относительная магнитная проницаемость среды, показывает, во сколько раз индукция магнитного поля в среде отличается от индукции в вакууме (В ₀), m₀ = 4p×10^-7 Н/м² (Гн/м) – магнитная постоянная.

7.3 Закон Био-Савара-Лапласа

Индукция магнитного поля В служит количественной характеристикой магнитного поля. Для количественного описания поля введем понятие элемента тока (в законе Ампера мы уже использовали это понятие).

Векторная величина, равная произведению силы тока I на длину прямолинейной части проводника dl, называется элементом тока . Направление элемента тока совпадает с направлением силы тока.

Рисунок 7.7

Элемент тока создает вокруг себя магнитное поле, величину и направление которого в каждой точке поля определяют с помощью закона Био-Савара-Лапласа. В скалярной форме закон Био-Савара-Лапласа можно представить в следующем виде:

. (7.4)

Закон Био-Савара-Лапласа утверждает, что элемент проводника с током создает в точке М магнитное поле, величина вектора индукции которого пропорциональна величине элемента тока 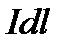, синусу угла a между направлением тока и радиус- вектором , определяющим положение точки М в пространстве, и обратно пропорциональна квадрату расстояния между элементом тока и точкой М (см. рис.7.7), – магнитная проницаемость среды, в которой распространяется поле, – магнитная проницаемость вакуума, которая равна .

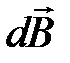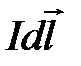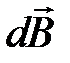Вектор перпендикулярен плоскости, образованной элементом тока и радиус-вектором , а направление определяется по правилу правой руки (см. рис.7.4б).

Для магнитных полей также соблюдается принцип суперпозиции:

при наложении нескольких магнитных полей, имеющих в данной точке пространства векторы индукции , вектор индукции результирующего поля равен геометрической (векторной) сумме векторов индукции, складываемых полей:

. (7.5)

Если происходит сложение двух полей 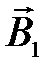и , то 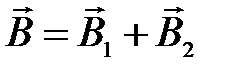, а абсолютное значение вектора индукции результирующего поля равно:

,

где a – угол между векторам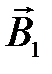и и .

Закон Био-Савара-Лапласа (7.4) представлен в виде дифференциального уравнения для вектора индукции магнитного поля, создаваемого не всем проводником, а лишь его небольшим участком dl. Для того чтобы вычислить полный вектор индукции в произвольной точке М, необходимо воспользоваться принципом суперпозиции (7.5). Вектор индукции магнитного поля, созданного бесконечно длинным проводником с током, в соответствии с принципом суперпозиции определяется уравнением

, (7.6)

где I – сила тока в проводнике, r – расстояние от проводника до исследуемой точки магнитного поля.

7.4 Сила Лоренца

Магнитное поле действует не только на проводники с током, но и на отдельные движущиеся заряженные частицы. Силу, действующую на движущуюся заряженную частицу, со стороны магнитного поля, называют силой Лоренца.

Сила, которую испытывает элемент тока в магнитном поле – это результирующая всех сил, действующих на отдельные заряды, движущиеся в выделенном элементе проводника с током и согласно уравнению (7.2) эта сила равна

.

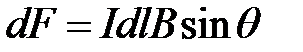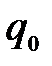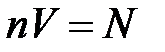Силу тока можно представить как количество заряда, протекающего в единицу времени через поперечное сечение проводника , где – величина заряда отдельной частицы, n -число частиц в единице объема Sdl. Величину dl можно представить как путь, пройденный заряженной частицей за единицу времени, тогда , dt – равно единице. Поэтому , где – объем элемента тока, – число носителей заряда в элементе тока

.

Тогда сила, действующая на отдельный заряд, движущийся в магнитном поле равна

. (7.7)

Чаще всего под силой Лоренца понимают силу, действующую на движущуюся заряженную частицу одновременно со стороны двух полей: электростатического и магнитного, тогда

.

Из формулы (7.7) видно, что магнитное поле не действует на заряженную частицу в двух случаях:

1) если частица неподвижна ,

2) если частица движется вдоль силовых линий магнитного поля .

Если частица влетает в магнитное поле перпендикулярно силовым линиям, 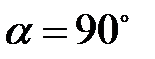, то сила Лоренца равна: .

Направление силы Лоренца определяется по правилу левой руки: если левую руку расположить так, чтобы силовые линии вектора магнитной индукции входили в ладонь, вытянутые пальцы показывали направление скорости, то отогнутый большой палец покажет направление силы, действующей на положительный заряд. Если частица имеет отрицательный заряд, то направление силы будет противоположным (см. рис.7.8).

Рисунок 7.8

Обозначим крестиками силовые линии магнитного поля, направленные перпендикулярно плоскости чертежа от нас. Сила Лоренца направлена перпендикулярно вектору скорости и вектору индукции, следовательно, является центростремительной силой. Под действием этой силы заряды будут двигаться по окружности, расположенной в плоскости перпендикулярной линиям индукции. Поскольку сила Лоренца является центростремительной силой, то

, (7.8)

где m – масса заряженной частицы, R – радиус окружности. Из формулы (7.8), следует, что радиус окружности, по которой движется в магнитном поле заряженная частица, определяется по формуле 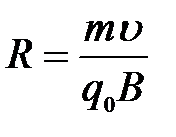, а период обращения частицы по этой окружности равен . Период не зависит от скорости движения заряженной частицы, а зависит только от ее массы. С помощью силы Лоренца можно разделить поток положительных и отрицательных частиц (см. рис.7.8). Сила Лоренца меняет направление скорости, не меняя ее величины. Следовательно, кинетическая энергия частицы не меняется. Значит, постоянное магнитное поле не совершает работы.

Поиск по сайту: