Электромагнитные волны. 9.1 Взаимные превращения электрических и магнитных полей

9.1 Взаимные превращения электрических и магнитных полей

Остановимся на природе ЭДС в случае изменения магнитного потока за счет изменения вектора индукции магнитного поля (1-й способ). Из сказанного в разделе 6.1, мы знаем, электродвижущая сила в любой цепи возникает только в том случае, если в этой цепи на заряды действуют какие-либо сторонние силы, т.е. силы не электростатического происхождения. Откуда следует, что чтобы возникла ЭДС, необходимо существование поля сторонних сил с напряженностью . Исходя из закона Ома в дифференциальной форме, плотность тока, возникающего в контуре, должна совпадать по направлению с напряженностью поля, т.к. контур, по которому течет индукционный ток замкнутый, то силовые линии этого поля должны быть тоже замкнутыми. Значит, это поле будет отличаться от электростатического поля. Силовые линии электростатического поля всегда разомкнуты; они начинаются и заканчиваются на электрических зарядах (см. раздел 5.3), и в соответствии с этим напряжение по замкнутому контуру в электростатическом поле всегда равно нулю. По этой причине электростатическое поле не может поддерживать замкнутое движение зарядов и, следовательно, не может привести к возникновению электродвижущей силы. Возникшее поле, имеющее замкнутые силовые линии, получило название вихревого электрического поля. Источником вихревого электрического поля является переменное магнитное поле.

Таким образом, углубленное истолкование явления электромагнитной индукции приводит к следующему выводу, выражающему первое основное положение Максвелла: всякое изменение магнитного поля вызывает появление вихревого электрического поля.

Анализируя различные электромагнитные процессы, Максвелл пришел к заключению, что должно существовать и обратное явление:

всякое изменение электрического поля вызывает появление вихревого магнитного поля. Это утверждение является вторым основным положением теории Максвелла.

Поскольку магнитное поле есть обязательный признак всякого тока (см. раздел 7.1), то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц. Ток смещения должен измеряться в тех же единицах, что и ток проводимости, поэтому количественно ток смещения можно оценить следующим образом:

,

где 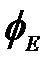поток вектора напряженности электрического поля. Таким образом, для получения магнитного поля не нужно иметь проводники с током. Магнитные и электрические поля могут существовать в пространстве в свободном состоянии, превращаясь одно в другое, причем эти поля взаимосвязаны. Совокупность взаимосвязанных электрического и магнитного полей называется электромагнитным полем.

9.2 Образование свободных электромагнитных волн

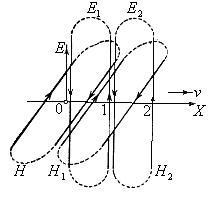Рисунок 9.1

Распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону, называется электромагнитной волной.

Представим себе, что в некоторой точке О (см.рис.9.1) создано каким- либо образом электрическое поле 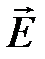. Если это поле не имеет источников его поддерживающих, то поле будет исчезать, но убывающее поле согласно Максвеллу вызывает магнитное поле 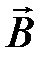, силовые линии которого направлены по часовой стрелке (глядя сверху на рисунке 9.1), т.к. в среде не имеется постоянных токов, поддерживающих магнитное поле, то это последнее будет исчезать и вызовет вихревое электрическое поле . Силовые линии этого поля будут направлены против часовой стрелки. Поле уничтожит первоначальное поле в точке О, но зато проявится в соседней точке 1. исчезая в точке 1, электрическое поле приведет к появлению магнитного поля , которое направлено как и поле . Поле уничтожит поле 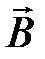и обнаружится в более удаленной точке и т.д. Таким образом, вместо первоначального поля мы получим и электрическое и магнитное поле, взаимно связанные друг с другом и распространяющиеся в пространстве, т.е. электромагнитную волну (см. рис.9.2) (вектор на рис. обозначен H).

Рисунок 9.2

Электромагнитную волну можно графически представить в виде двух синусоид, лежащих во взаимно перпендикулярных плоскостях (см. рис.9.2). Одна синусоида отражает колебания вектора напряженности электрического поля, другая - вектора индукции магнитного поля. Вектор скорости распространения электромагнитной волны будет перпендикулярен векторам и (или )

,

.

Эти формулы выражают закон изменения электрического и магнитного полей в электромагнитной волне, распространяющейся в направлении х. Они называются уравнением электромагнитной волны, где с – скорость распространения электромагнитной волны в вакууме.

Поиск по сайту: