О НЕКОТОРЫХ СВОЙСТВАХ НЕПРЕРЫВНЫХ СИГНАЛОВ

ЧАСТОТНО-ВРЕМЕННОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Известно, что некоторая функция x(t) и ее спектр X() однозначно выражаются друг через друга (см. формулы (8) и (9) п. 5.4). Следовательно, сигнал можно рассматривать в любом из этих эквивалентных представлений — временном или частотном. При этом масштабные параметры этих представлений связаны обратно пропорциональной зависимостью. Пусть x(t) имеет спектр X(). Изменим масштаб по оси времени в а раз (например, воспроизведем запись x(t) с другой скоростью) и найдем спектр функции x(at):

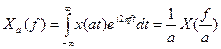. (1)

Масштаб по частотной оси изменился в 1/a раз. Более того, из свойств преобразования Фурье следует, что сигналы с ограниченной длительностью имеют спектры неограниченной ширины, а сигналы с ограниченной полосой частот длятся бесконечно долго.

Этот математический результат находится в противоречии с практикой: в реальности все сигналы конечны по длительности, а все чувствительные к сигналам устройства не могут воспринимать и воспроизводить абсолютно все частоты. Например, диапазон частот, к которым чувствителен слух человека, простирается от нескольких герц до 20 — 30 кГц, а все различимые звуки человеческой речи длятся доли секунды.

Говорить об одновременной ограниченности сигналов и по времени, и по спектру оказывается возможным при использовании энергетического критерия точности: сигнал считается имеющим конечную длительность Т, если в этом интервале времени сосредоточена основная часть всей энергии функции x(t); в то же время и ширина спектра F сигнала определяется как область частот, содержащая эту же часть всей энергии спектра X():

, (2)

Здесь величина 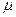меньше единицы, но достаточно близка к ней, а величина 1- 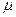характеризует косвенным образом точность, о которой шла речь.

Теперь можно говорить о том, какую "площадь" на плоскости "частота — время" занимает тот или иной сигнал. Если строго, следовать теории Фурье-преобразований, то получим, что эта площадь для всех сигналов бесконечна, но для большинства из них энергетический критерий позволит ограничить ее естественным образом (рис.5.1.).

Рис.5.1. Иллюстрация частотно-временной неопределенности сигнала

Меняя форму сигнала s(t), можно менять и занимаемую им площадь. Оказывается, что уменьшать эту площадь можно лишь до некоторого предела. Этот предел достигается на кривой, являющейся гармоническим колебанием, которое модулировано по амплитуде гауссовым импульсом; интересно, что спектр этой кривой имеет такую же форму:

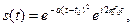(3)

(4)

Существование предела, ниже которого нельзя сжать площадь сигнала, занимаемую им на плоскости "частота — время", и называется принципом частотно-временной неопределенности сигналов:

(5)

ДИСКРЕТНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Вторым важным аспектом теории сигналов является проблема дискретного представления непрерывных сигналов. Вопрос формулируется так: существуют ли условия (и если да, то каковы они), при которых любой непрерывной функции x(t) можно поставить во взаимно однозначное соответствие дискретное множество чисел , k =... -2, - 1, 0, 1, 2,...? Ограничимся более конкретной формулировкой поставленной задачи и рассмотрим условия выполнения равенства

(6)

Функции называются координатными функциями, они не должны зависеть от x(t), более того, они заранее известны. Ряд в правой части равенства называется разложением x(t) по координатным функциям. Числовые коэффициенты содержат всю информацию об х(t), необходимую для восстановления этой функции по формуле (6); следовательно, являются функционалами* от функции x(t).

(Функционалом называется отображение множества функций в множество чисел).

Наиболее известны разложения по системе ортогональных и нормированных функций. Это означает, что функции удовлетворяют условиям

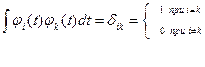(7)

Умножим обе части равенства (6) на и проинтегрируем (опуская тонкости, будем считать, что все операции обоснованы):

(8)

Такое представление называют рядом Фурье, а (x) — коэффициентами Фурье. Условия сходимости ряда Фурье к функции х(t) подробно исследованы и, кратко говоря, сводятся к тому, чтобы были оправданы все необходимые математические операции, а коэффициенты Фурье убывали достаточно быстро (точнее, 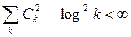). Это не очень жесткое ограничение, но все же оно связывает свойства системы координатных функций и самих функций x(t). Например, если — гармонические функции кратных частот, то x(t) должна быть периодической функцией с периодом Т, равным периоду самой низкочастотной гapмоники:

, (9)

. (10)

Значительный интерес привлекли разложения реализаций случайного процесса с ограниченной полосой частот. Для таких сигналов В.А. Котельников доказал (1946) следующую теорему (теорему отсчетов):

любая функция со спектром, находящимся в интервале [0, F ], полностью определяется последовательностью ее значений в тачках, отстоящих друг от друга на 1/ (2F) единиц времени.

Итак, из многочисленных результатов теории сигналов мы выделяем два, как существенно поясняющие природу непрерывных сигналов. Первый состоит в том, что сигналы обнаруживают своеобразную "упругость" занимаемой ими площади на плоскости "частота — время". Это явление называется частотно-временной неопределенностью сигналов. Второй результат заключается в том, что определенный класс непрерывных сигналов допускает взаимно однозначное соответствие между любой реализацией из этого класса и дискретным набором отсчетов данной реализации.

Поиск по сайту: