Изучение методик расчета случайных величин в Excel

Цель работы: исследование законов распределения случайных величин с использованием средств пакета Excel.

Задание на выполнение работы: решить задачи, условия которых изложены в описании, построить графики распределений, а также построить всекривые распределений на одном графике

Теоретические сведения:

Количественной характеристикой результата случайного явления служит случайная переменная величина, численное значение которой не может быть указано до постановки и проведения опыта. Конкретное значение, которое случайная величина принимает в результате данного опыта, называется ее реализацией. Дискретная случайная величина в определенном промежутке может принимать ограниченное, конечное число значений. Для полной характеристики случайной величины необходимо указывать не только все возможные значения, но и распределение вероятности того, что случайная величина примет одно из этих значений, иными словами, необходимо указать закон распределения вероятностей значений случайной величины. Закон распределения случайной величины – это заданная в той или иной форме связь между возможными значениями случайной величины и соответствующими им возможностями их появления.

Рассмотрим некоторые типичные законы распределения дискретных случайных величин.

БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Функция вероятности 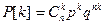, где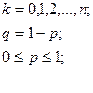

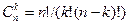- коэффициенты разложения бинома

Биномиальный закон выражает распределение числа k появлений некоторого события в n повторных независимых испытаниях, если при каждом испытании вероятность появления события остается неизменной и равной р.

ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ

Функция вероятности 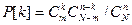, где - коэффициенты разложения бинома, .

Гипергеометрическое распределение имеет число годных изделий К в пробе, содержащей n образцов, взятой из партии N изделий, среди которых имеется m бездефектных.

РАСПРЕДЕЛЕНИЕ ПУАССОНА

Функция вероятности , где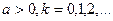

Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например, количество машин, появляющихся на площади за 1 минуту.

Порядок выполнения работы:

В пакете Excel команда, позволяющая расчитать вероятность события, подчиняющегося биномиальному закону распределения вероятностей записывается как

БИНОМРАСП (число_успехов; число_испытаний; вероятность_успеха; интегральная)

Число_успехов - это количество успешных испытаний.

Число_испытаний - это число независимых испытаний.

Вероятность_успеха - это вероятность успеха каждого испытания.

Интегральная - это логическое значение, определяющее форму функции. Если аргумент интегральная имеет значение ИСТИНА, то функция БИНОМРАСП возвращает интегральную функцию распределения, то есть вероятность того, что число успешных испытаний не менее значения аргумента число_успехов; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция распределения, то есть вероятность того, что число успешных испытаний в точности равно значению аргумента число_успехов.

Пример

При бросании монеты может выпасть орел или решка. Вероятность того, что при первом бросании выпадет орел, равна 0,5, а вероятность того, что в точности 6 раз из 10 выпадет орел составит:

БИНОМРАСП(6;10;0,5;ЛОЖЬ) равняется 0,205078

Задача: Вероятность выбора наудачу из большой партии изделия с параметром, имеющим отклонение в плюс от номинала, составляет р=1/2. Найти вероятность появления 1,2,3,4,5 таких изделий в пробе из 5 экземпляров. Построить график зависимости вероятности от числа изделий.

В пакете Excel команда, позволяющая расчитать вероятность события, подчиняющегося гипергеометрическому закону распределения вероятностей записывается как

ГИПЕРГЕОМЕТ (число_успехов_в_выборке; размер_выборки; число_успехов_в_совокупности; размер_совокупности)

Число_успехов_в_выборке - это количество успешных испытаний в выборке.

Размер_выборки - это размер выборки.

Число_успехов_в_совокупности - это количество успешных испытаний в генеральной совокупности.

Размер_совокупности - это размер генеральной совокупности.

Пример

В коробке 20 конфет. Восемь из них карамельки, а остальные 12 - орешки. Если некто выбирает 4 конфеты наугад, то следующая функция вернет вероятность того, что в точности одна конфета окажется карамелькой.

ГИПЕРГЕОМЕТ(1;4;8;20) равняется 0,363261

Задача: В партии из 9 изделий имеется 5 бездефектных. Найти вероятность того, что в пробе из 4 изделий будет 1, 2, 3, 4 бездефектных. Построить график зависимости вероятности от числа бездефектных изделий.

В пакете Excel команда, позволяющая расчитать вероятность события, подчиняющегося закону распределения вероятностей Пуассона записывается как

ПУАССОН (x; среднее; интегральная)

X - это количество событий.

Среднее - это ожидаемое численное значение.

Интегральная - это логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент интегральная имеет значение ИСТИНА, то функция ПУАССОН возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий будет от 0 до x включительно; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность того, что событий будет в точности x.

Поиск по сайту: