 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Глава 1.СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР)
Уравнение такой системы имеет вид:
 (1.1)
(1.1)
(примерами могут служить математический маятник при малых углах отклонения и идеальный колебательный контур). Решим уравнение (1.1) подробно, пользуясь классическим методом Эйлера. Ищем частное решение в виде:
 , (1.2)
, (1.2)
где 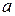 и
и  – постоянные, пока неизвестные константы. Подставим (1.2) в уравнение (1.1)
– постоянные, пока неизвестные константы. Подставим (1.2) в уравнение (1.1)
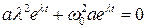 . (1.3)
. (1.3)
Разделим обе части уравнения на 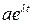 и получим алгебраическое, так называемое характеристическое, уравнение:
и получим алгебраическое, так называемое характеристическое, уравнение:
 . (1.4)
. (1.4)
Корни этого уравнения
 , (1.5)
, (1.5)
 , (1.6)
, (1.6)
где  – мнимая единица. Корни мнимые и комплексно-сопряжённые.
– мнимая единица. Корни мнимые и комплексно-сопряжённые.
Как известно, общее решение есть сумма частных, т.е.
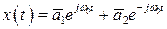 . (1.7)
. (1.7)
Мы полагаем, что  есть действительная величина. Чтобы это выполнялось, постоянные
есть действительная величина. Чтобы это выполнялось, постоянные  и
и  должны быть комплексно сопряженными, т.е.
должны быть комплексно сопряженными, т.е.
 . (1.8)
. (1.8)
Две постоянные 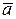 и
и  определяются из двух начальных условий:
определяются из двух начальных условий:
 ,
, 
Решение в форме (1.8) преимущественно используется в теории; для прикладных задач оно не удобно, так как 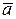 и
и  не измеряются. Перейдём к форме решения, которое наиболее употребительно на практике. Представим комплексные постоянные в полярной форме:
не измеряются. Перейдём к форме решения, которое наиболее употребительно на практике. Представим комплексные постоянные в полярной форме:
 , (1.9)
, (1.9)
 . (1.10)
. (1.10)
Подставим их в (1.8) и воспользуемся формулой Эйлера
 , (1.11)
, (1.11)
тогда
 , (1.12)
, (1.12)
где  - амплитуда колебаний,
- амплитуда колебаний, 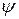 - начальная фаза.
- начальная фаза.
 и
и 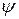 определяются из начальных условий. Заметим, что начальная фаза зависит от начала отсчёта во времени. Действительно, постоянную
определяются из начальных условий. Заметим, что начальная фаза зависит от начала отсчёта во времени. Действительно, постоянную 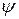 можно представить в виде:
можно представить в виде:
 , (1.13)
, (1.13)
тогда
 . (1.14)
. (1.14)
Если начало отсчёта во времени совпадает с  , начальная фаза равна нулю. Для гармонического колебания сдвиг по фазе и сдвиг во времени эквивалентны.
, начальная фаза равна нулю. Для гармонического колебания сдвиг по фазе и сдвиг во времени эквивалентны.
Разложим косинус в (1.13) на косинусоидальную и синусоидальную составляющие. Получим ещё одно представление:
 , (1.15)
, (1.15)
где
 , (1.16)
, (1.16)
 . (1.17)
. (1.17)
Если 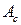 и
и 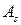 известны, то нетрудно найти амплитуду и фазу колебания, используя следующие соотношения:
известны, то нетрудно найти амплитуду и фазу колебания, используя следующие соотношения:
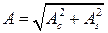 ,
,  . (1.18)
. (1.18)
Все три формы записи (1.8, 1.12, 1.15) эквивалентны. Использование конкретной формы определяется удобством рассмотрения конкретной задачи.
Анализируя решение, можно сказать, что собственные колебания гармонического осциллятора есть гармоническое колебание, частота которого зависит от параметров системы и не зависит от начальных условий; от начальных условий зависят амплитуда и начальная фаза.
Независимость от начальных условий частоты (периода) собственных колебаний называется изохорностью.
Рассмотрим энергию гармонического осциллятора на примере колебательного контура. Уравнение движения в контуре
 . (1.19)
. (1.19)
Умножим слагаемые этого уравнения на 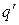 :
:
 . (1.20)
. (1.20)
После преобразования его можно представить в виде:
 . (1.21)
. (1.21)
Так как 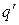 есть ток
есть ток  , то
, то
 , (1.22)
, (1.22)
где  -есть мгновенное значение магнитной энергии в индуктивности, а
-есть мгновенное значение магнитной энергии в индуктивности, а  –электрической энергии в ёмкости.
–электрической энергии в ёмкости.
Полная энергия, запасенная контуром:
 . (1.23)
. (1.23)
Из (1.7) получим  , т.е.
, т.е.  - энергия контура остается постоянной, не зависит от времени. Мы приходим к выводу, что система консервативна.
- энергия контура остается постоянной, не зависит от времени. Мы приходим к выводу, что система консервативна.
Что же происходит с магнитной и электрической энергией в отдельности? Закон изменения заряда на конденсаторе нам известен – (1.12) и
 , (1.24)
, (1.24)
тогда
 . (1.25)
. (1.25)
Найдем закон изменения энергии в конденсаторе. Ток в емкостной ветви можно найти используя следующее выражение
 . (1.26)
. (1.26)
Подставив (1.28) в формулу для нахождения электрической энергии получим закон изменения электрической энергии на конденсаторе
 , (1.27)
, (1.27)
 . (1.28)
. (1.28)
С учетом
 (1.29)
(1.29)
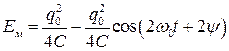 . (1.30)
. (1.30)
Таким образом, энергия в каждом элементе контура колеблется с удвоенной частотой. График этих колебаний приведен на рис. 6.
 В начальный момент времени вся энергия сосредоточена в емкости, магнитная энергия ровна нулю. По мере разряда емкости через индуктивность электрическая энергия из емкости переходит в магнитную энергию индуктивности. Через четверть периода вся энергия сосредотачивается в индуктивности, т.е. емкость полностью разрядилась. Затем этот процесс периодически повторяется.
В начальный момент времени вся энергия сосредоточена в емкости, магнитная энергия ровна нулю. По мере разряда емкости через индуктивность электрическая энергия из емкости переходит в магнитную энергию индуктивности. Через четверть периода вся энергия сосредотачивается в индуктивности, т.е. емкость полностью разрядилась. Затем этот процесс периодически повторяется.
Таким образом, колебание в идеальном контуре – это переход электрической энергии в магнитную и обратно, периодически повторяющийся во времени.
Этот вывод справедлив для любых электромагнитных колебательных систем, в частности для объемных резонаторов, где магнитная и электрическая энергия пространственно не разделены.
Обобщая этот результат, можно утверждать, что колебательный процесс в линейной консервативной системе – это периодический переход энергии одного типа в другой. Так, при колебаниях маятника кинетическая энергия переходит в потенциальную и наоборот.
Поиск по сайту: