С тремя неизвестными

Однородная система трех линейных уравнений с тремя неизвестными имеет вид:

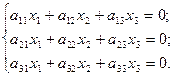
Данная система будет иметь ненулевые решения лишь в том случае, когда определитель системы будет равен нулю. Отбрасывая одно из уравнений, мы получим однородную систему двух линейных уравнений с тремя неизвестными, методика решения которой уже разобрана ранее.

П р и м е р. Решить систему линейных уравнений:

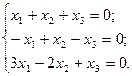
Решение:

Находим определитель D:

.

Поскольку определитель D отличный от нуля, система имеет нулевое решение.

Ответ: х₁ = 0; х₂ = 0; х₃ = 0.

П р и м е р. Решить систему линейных уравнений:

Решение:

Находим определитель D:

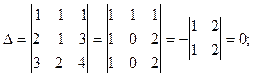
Поскольку D=0, то следовательно, система имеет ненулевые решения. Отбрасывая третье уравнение, получим следующую систему:

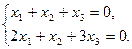
Найдем решение системы, используя методику решения однородной системы двух линейных уравнений с тремя неизвестными.

;

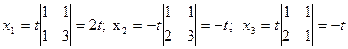При t =1, получим решение: х₁ = 2; х₂ = -1; х₃ = -1.

Проверка показывает, что это решение удовлетворяет отброшенное третье уравнение и является решением исходной системы.

Ответ: Множество решений. Одно из частных решений: х₁ = 2; х₂ = -1; х₃ = -1.

Поиск по сайту: