ОЛДУ с постоянными коэффициентами

Рассмотрим ОЛДУ -го порядка с постоянными коэффициентами.

. (1)

Покажем, что это уравнение всегда может быть проинтегрировано в элементарных функциях. Для этого построим фундаментальную систему решений данного уравнения. Попытаемся найти частное решение уравнения (1) вида . Имеем , , …, , , поэтому

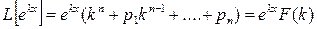, где .

Уравнение называется характеристическим уравнением ОЛДУ (1).

Многочлен 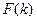называется характеристическим многочленом, а его корни – характеристическими числами уравнения (1). Так как 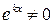, то будет решением (1) тогда и только тогда, когда .

Таким образом, доказана

Теорема 1. Пусть действительное число есть характеристическое число ОЛДУ (1). Тогда есть его решение.

Следствие 1. Если характеристическое уравнение ОЛДУ (1) имеет различных действительных корней , то функции , …,

образуют фундаментальную систему его решений.

Действительно,

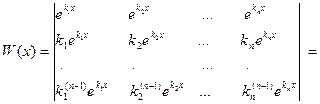
Определитель

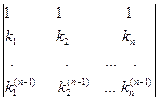
есть определитель Вандермонда. Он равен .Следовательно, Поэтому функции , …, линейно независимы.

Характеристический многочлен ОЛДУ (1) есть многочлен с действительными коэффициентами. Его корнями могут быть комплексные числа. Для того, чтобы выяснить, какие решения уравнения (1) отвечают простому комплексному корню характеристического уравнения, мы будем рассматривать комплексные функции действительного переменного . Определяя для этих функций производную так же, как для действительных функций действительного переменного, мы придем к тому, что 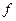дифференцируема тогда и только тогда, когда дифференцируемы функции и . При этом . Поэтому и тем самым . Так как также есть характеристическое число ОЛДУ (1), то 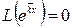. Но тогда

, , , .

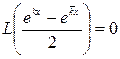Таким образом, каждый простой корень характеристического уравнения ОЛДУ (1) дает два действительных решения и решения (1). Функции и линейно независимы.

Допустим теперь, что есть корень кратности характеристического уравнения ОЛДУ (1). Тогда , где . Действительно,

для корня кратности 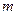имеем

Можно показать, что

.

Поэтому . Если , то решениями ОЛДУ (1) будут функции

, , …, ,

, , …, .

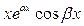Если вещественный корень, то решениями будут .

Можно показать, что указанные решения ОЛДУ (1), отвечающие корню характеристического уравнения кратности 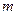линейно независимы.

Теорема 2. Для построения фундаментальной системы решений уравнения (1) необходимо найти корни характеристического уравнения, определить их кратности, и для каждого корня с учетом его кратности выписать решения, указанные выше. Все вместе эти решения составят фундаментальную систему решений уравнения (1).

12) Линейные неоднородные уравнения.

Для линейного неоднородного уравнения

(1)

справедлива следующая

Теорема 1. Сумма общего решения уравнения однородного уравнения

и какого-либо частного решения уравнения (1) есть общее решение уравнения (1).

Не всегда удается подобрать частное решение. Поэтому большое значение имеет метод вариации постоянных, дающий возможность проинтегрировать НЛДУ , если известна фундаментальная система решений соответствующего однородного уравнения .

Пусть – фундаментальная система уравнения (1'). Будем искать решение уравнения в виде

(2)

Потребуем, чтобы

(3),

Тогда

(4)

Подчиним условию

(5)

Тогда

(6)

и т.д. После того, как выполнены условия

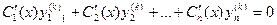
, (7)

производная функции (2) запишется в виде

.

Наконец, потребовав, чтобы

(8)

мы получим

Итак, если функции подчинены условиям (7) и (8), то

,

, '

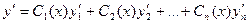…………………………………….. (9)

,

Тогда

Таким образом, функция

,

при условии, что подчинены условиям (7) и (8), является решением дифференциального уравнения (1).

Условия (7) и (8) представляют собой систему

Это система линейных уравнений с неизвестными . Так как определитель этой системы есть определитель Вронского 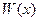линейно независимой системы функций 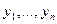, то функции могут быть найдены по правилу Крамера. Но тогда интегрированием мы определим и функции .

13) НЛДУ с постоянными коэффициентами.

Другой метод интегрирования – метод неопределенных коэффициентов – применяется для НЛДУ с постоянными коэффициентами.

. (1)

Приведем сводную таблицу видов частных решений для различных видов правых частей. Через будем обозначать многочлен с действительными коэффициентами степени 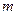. Напомним, что

Сводная таблица видов частных решений НЛДУ с постоянными коэффициентами для различных видов правых частей.

Поиск по сайту: