АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Энергия колебаний струны

Читайте также:
  1. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  2. Алекс встал перед съёмочной группой, надел ремень гитары через голову и поставил руку на струны.
  3. Амплитуда, период, частота, фаза колебаний.
  4. Анализ сезонных колебаний
  5. Анализ сезонных колебаний товарооборота
  6. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  7. Виды колебаний
  8. Внутренняя энергия идеального газа
  9. Внутренняя энергия идеального газа. Работа газа при изобарном расширении. Применение первого начала термодинамики к изопроцессам. Понятие о втором начале термодинамики.
  10. Внутренняя энергия реального газа
  11. Внутренняя энергия реального газа. Эффект Джоуля - Томсона
  12. Внутренняя энергия тела и способы её изменения. Изменение внутренней энергии тела при нагревании. Первое начало термодинамики. Обратимые и необратимые процессы.

Найдем выражение для энергии поперечных колебаний струны , где -кинетическая и -потенциальная энергия. Элемент струны , движущийся со скоростью , обладает кинетической энергией:

.

Кинетическая энергия всей струны равна:

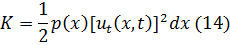
Потенциальная энергия поперечных колебаний струны, имеющей при форму , равна работе, которую надо совершить, чтобы струна перешла из положения равновесия в положение Пусть функция дает профиль струны в момент , причем

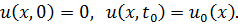
Элемент под действием равнодействующей сил натяжения

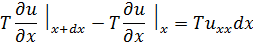
За время проходит путь . Работа, производимая всей струной за время проходит путь , равна

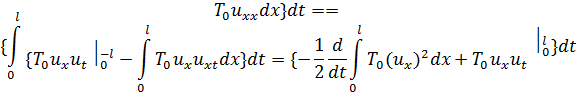
Интегрируя по от 0 до 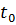, получаем:

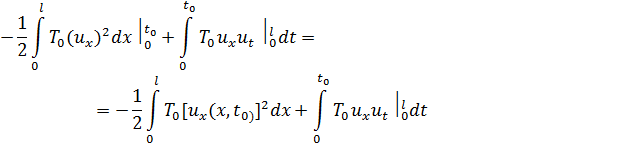
Нетрудно выяснить смысл последнего слагаемого правой части этого равенства. Действительно, есть величина натяжения на конце струны x=0; -перемещение этого конца, а интеграл

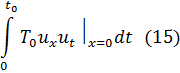
Представляет работу, которую надо затратить на перемещение конца x=0. Аналогичный имеет слагаемое, соответствующее . Если концы струны закреплены, то работа на концах струны будет равна нулю(при этом . Следовательно, при перемещении закрепленной на концах струны из положения равновесия в положение работа не зависит от способа перевода струны в это положение и равна:

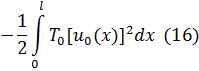
Потенциальной энергии струны в момент с обратным знаком. Таким образом, полная энергия струны равна:

 

 

 

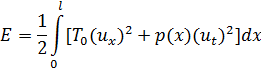
Вывод

Список литературы

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)