 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача Д6
(тема: “Принцип Даламбера для механической системы”)
Вертикальный вал  (рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью
(рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью  с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 (
с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 ( ). К валу жестко прикреплены невесомый стержень 1 длиной
). К валу жестко прикреплены невесомый стержень 1 длиной  м с точечной массой
м с точечной массой  кг на конце и однородный стержень 2 длиной
кг на конце и однородный стержень 2 длиной  м, имеющий массу
м, имеющий массу  кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять
кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять  м.
м.
Перед выполнением задания прочтите по учебнику тему: «Принцип Даламбера». Ответьте на вопросы:
1. Сформулируйте принцип Даламбера для точки.
2. Как определяется модуль и направление силы инерции для точки? В каких случаях сила инерции равна нулю?
3. Сформулируйте принцип Даламбера для системы.
4. Чему равны главный вектор и главный момент сил инерции системы?
5. Запишите уравнения равновесия произвольной системы сил и плоской системы сил в координатной форме (вспомнив соответствующие уравнения статики).
Принцип Даламбера для точки и системы
(краткие сведения из теории)
Принцип Даламбера для точки.Рассмотрим дифференциальное уравнение движения точки в инерциальной системе отсчета в векторной форме:
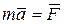 , (1)
где , (1)
где 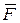 – векторная сумма всех сил, действующих на точку (активных и реакций связей). Перенесем вектор – векторная сумма всех сил, действующих на точку (активных и реакций связей). Перенесем вектор 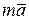 в правую часть уравнения (1): в правую часть уравнения (1):  ; обозначим ; обозначим  ; тогда получим уравнение ; тогда получим уравнение
 , (2)
где , (2)
где
 ; (3)
эта величина называется силой инерции точки.
Уравнение (2) по форме соответствует уравнению равновесия сил в векторной форме. В этом и состоит принцип Даламбера для точки: если к приложенным к точке силам добавить силу инерции (3), то полученная система сил (активных, реакций связей и сил инерции) будет уравновешенной и задачу динамики можно решать, применив методы статики.
Такой метод решения задач динамики называется методом кинетостатики. ; (3)
эта величина называется силой инерции точки.
Уравнение (2) по форме соответствует уравнению равновесия сил в векторной форме. В этом и состоит принцип Даламбера для точки: если к приложенным к точке силам добавить силу инерции (3), то полученная система сил (активных, реакций связей и сил инерции) будет уравновешенной и задачу динамики можно решать, применив методы статики.
Такой метод решения задач динамики называется методом кинетостатики.
|
Сила инерции точки  (см. (3)). Модуль силы инерции точки равен (см. (3)). Модуль силы инерции точки равен  ; направлена сила инерции ; направлена сила инерции  в сторону, противоположную абсолютному ускорению точки в сторону, противоположную абсолютному ускорению точки  . Поэтому для построения . Поэтому для построения  на рисунке следует сначала построить вектор на рисунке следует сначала построить вектор  (или его составляющие, например, (или его составляющие, например,  и и  ), и затем построить ), и затем построить  в сторону, противоположную вектору в сторону, противоположную вектору  (или (или  и и  в стороны, противоположные в стороны, противоположные  и и  , соответственно).
Принцип Даламбера для системы. Применим описанный выше принцип Даламбера к каждой точке системы. К силам, действующим на каждую точку (внешним и внутренним), добавляется сила инерции (3). Получаем систему сил (внешних, внутренних и сил инерции) для всех точек системы.
Принцип Даламбера для системы формулируется следующим образом: если к внешним силам (активным и реакциям связей), действующим на каждую точку системы, добавить силу инерции (3), то полученная система сил будет уравновешенной и для нее справедливы уравнения статики.
Уравнения равновесия сил (внешних (активных и реакций связей) и сил инерции) в векторной форме: , соответственно).
Принцип Даламбера для системы. Применим описанный выше принцип Даламбера к каждой точке системы. К силам, действующим на каждую точку (внешним и внутренним), добавляется сила инерции (3). Получаем систему сил (внешних, внутренних и сил инерции) для всех точек системы.
Принцип Даламбера для системы формулируется следующим образом: если к внешним силам (активным и реакциям связей), действующим на каждую точку системы, добавить силу инерции (3), то полученная система сил будет уравновешенной и для нее справедливы уравнения статики.
Уравнения равновесия сил (внешних (активных и реакций связей) и сил инерции) в векторной форме:
 ; ;
 ,
где ,
где  , , – главный вектор и главный момент относительно произвольного центра O внешних сил (активных и реакций связей); – главный вектор и главный момент относительно произвольного центра O внешних сил (активных и реакций связей);  , ,  – главный вектор и главный момент относительно произвольного центра O сил инерции. В алгебраической (координатной) форме уравнения равновесия записываются различным образом, в зависимости от типа получившейся системы сил (произвольная система сил, плоская система сил и т. д., см. раздел “Статика”).
Главный вектор сил инерции не зависит от центра приведения и может быть вычислен заранее: – главный вектор и главный момент относительно произвольного центра O сил инерции. В алгебраической (координатной) форме уравнения равновесия записываются различным образом, в зависимости от типа получившейся системы сил (произвольная система сил, плоская система сил и т. д., см. раздел “Статика”).
Главный вектор сил инерции не зависит от центра приведения и может быть вычислен заранее:
 ,
где M – масса тела (системы), ,
где M – масса тела (системы),  – абсолютное ускорение центра масс тела (системы). Главный вектор не обязательно приложен в центре масс (так как центр приведения – произвольная точка).
Главный момент сил инерции относительно центра приведения O: – абсолютное ускорение центра масс тела (системы). Главный вектор не обязательно приложен в центре масс (так как центр приведения – произвольная точка).
Главный момент сил инерции относительно центра приведения O:
 .
Главный момент зависит от центра приведения O и заранее может быть вычислен только в некоторых частных случаях (для некоторых видов движения тела и различных центров приведения). .
Главный момент зависит от центра приведения O и заранее может быть вычислен только в некоторых частных случаях (для некоторых видов движения тела и различных центров приведения).
|

| ||||||

| ||||||

|
Таблица Д6
| Номер условия | Подшипник в точке | Крепление | a, град. | b, град. | |
| стержня 1 в точке | стержня 2 в точке | ||||
| В | D | K | |||
| D | B | E | |||
| E | D | B | |||
| K | D | E | |||
| B | E | D | |||
| D | K | B | |||
| E | B | K | |||
| K | E | B | |||
| D | E | K | |||
| E | K | D |
Указания. Задача Д6 – на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что система сил инерции точек стержня 2 представляет собой систему параллельных сил, направленных в одну сторону и, следовательно, имеет равнодействующую  . Модуль равнодействующей
. Модуль равнодействующей  , где
, где  – ускорение центра масс С стержня. Линия действия силы
– ускорение центра масс С стержня. Линия действия силы  не проходит через точку С, так как силы инерции образуют линейно распределенную нагрузку(см. пример Д6).
не проходит через точку С, так как силы инерции образуют линейно распределенную нагрузку(см. пример Д6).

| Пример Д6. С невесомым валом  , вращающимся с постоянной угловой скоростью , вращающимся с постоянной угловой скоростью  , жестко скреплен однородный стержень , жестко скреплен однородный стержень  длиной длиной  и массой и массой  , имеющий на конце груз массой , имеющий на конце груз массой  (рис. Д6).
Дано: (рис. Д6).
Дано:  м, м,  м, м, 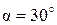 , ,
 м, м,  кг, кг,  кг, кг,  с-1.
Определить: реакции подпятника с-1.
Определить: реакции подпятника 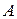 и подшипника и подшипника  . .
|
Решение. Для определения искомых реакций рассмотрим движение механической системы, состоящейиз вала  , стержня
, стержня  и груза, и применим принцип Даламбера. Проведем неподвижныеоси
и груза, и применим принцип Даламбера. Проведем неподвижныеоси  , лежащие в данный момент времени в плоскости, образуемой валом и стержнем, и изобразим действующие на систему внешние силы: силы тяжести
, лежащие в данный момент времени в плоскости, образуемой валом и стержнем, и изобразим действующие на систему внешние силы: силы тяжести 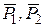 , составляющие
, составляющие  реакции подпятника и реакцию
реакции подпятника и реакцию  подшипника (XA, YA, XB надо определить).
подшипника (XA, YA, XB надо определить).
Согласно принципу Даламбера, присоединим к этим силам силы инерции точек стержня и груза, считая груз материальной точкой. Так как вал вращается равномерно ( ), то точки стержня имеют только нормальные ускорения
), то точки стержня имеют только нормальные ускорения 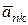 направленные к оси вращения; численно
направленные к оси вращения; численно 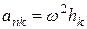 , где
, где  – расстояние от точки от оси. Тогда силы инерции
– расстояние от точки от оси. Тогда силы инерции  будут направлены от оси вращения; численно
будут направлены от оси вращения; численно  , где mk – масса точки. Поскольку
, где mk – масса точки. Поскольку  пропорциональны
пропорциональны  , то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей
, то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей  , линия действия которой проходит через центр тяжести этого треугольника (точку пересечения медиан), т.е. на расстоянии H 1 от вершины О, где
, линия действия которой проходит через центр тяжести этого треугольника (точку пересечения медиан), т.е. на расстоянии H 1 от вершины О, где 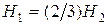 ,
, 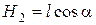 (см. рис. Д6).
(см. рис. Д6).
Известно, что равнодействующая любой системы сил равна ее главному вектору; численно главный вектор сил инерции стержня  , где
, где  – ускорение центра масс стержня. Так как стержень вращается с постоянной угловой скоростью, то ускорение
– ускорение центра масс стержня. Так как стержень вращается с постоянной угловой скоростью, то ускорение  центра масс стержня имеет только нормальную составляющую:
центра масс стержня имеет только нормальную составляющую:  . В результате получим
. В результате получим 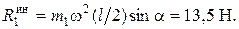
Аналогично для силы инерции  груза найдем, что она направлена от оси вращения; численно
груза найдем, что она направлена от оси вращения; численно 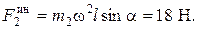
Так как все действующие силы и силы инерции лежат в плоскости Aху, то и реакции подпятника А и подшипника В тоже лежат в этой плоскости, что было учтено приих изображении на рисунке.
По принципу Даламбера, приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составляя для этой плоской системы сил три уравнения равновесия, получим:
 (1)
(1)
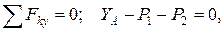 (2)
(2)
 (3)
(3)
Подставив сюда числовые значения всех заданных и вычисленных величин и решив эту систему уравнений, найдем искомые реакции (в своей задаче решение уравнений равновесия должно быть выполнено подробно).
Ответ: XA = -11,8 Н, YA = 49,1 Н, XB = -19,7 Н.
Знаки указывают, что силы 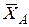 и
и  направлены противоположно показанным на рис. Д6.
направлены противоположно показанным на рис. Д6.
Поиск по сайту: