Воспроизводящая функция представляется аппроксимирующим полиномом

где {j_j(t)} - система базисных функций.

При одном и том же операторе представления А для восстановления могут использоваться различные операторы В.

Из соотношений (2.3) и (2.4) следует, что произведения [ξ_j(t)φ_j(t)] должны иметь размерность, обратную времени.

Методы дискретизации в первую очередь разделяются в зависимости от способа получения координат сигнала.

В случае, когда в качестве весовых функций используются базисные функции [ (t) = j_j(t)], координаты с₁, c₂,..., c_N сигнала u(t) получаются «взвешенным» интегрированием сигнала на некотором интервале времени Т. При этом предполагается, что базисные функции ортогональны и обеспечивают сходимость в среднеквадратичном ряде (2.4) к u(t) при N [условие (1.8)], что дает возможность ограничить число координат в соответствии с заданной погрешностью восстановления.

Предъявляя дополнительные требования к базисным функциям, можно провести дискретизацию различных моделей сигнала. Хотя дискретизации всегда подвергается конкретная реализация случайного процесса и, следовательно, детермированная функция, в большинстве случаев алгоритм дискретизации выбирают неизменным для всего множества реализаций и поэтому он должен опираться на характеристики случайного процесса как модели сигнала.

Методы дискретизации следует рассматривать как с позиций полезности для решения теоретических вопросов передачи и преобразования сигналов, так и с позиций возможности их технической реализации. В теоретическом плане весьма важны методы дискретизации, обеспечивающие минимальное число координат при заданной погрешности воспроизведения. Их называют методами оптимальной или предельной дискретизации.

Если за модель сигнала принять нестационарный случайный процесс, как наиболее полно отражающий свойства реального сигнала, некоррелированность координат, а следовательно, и их минимальное число обеспечивают каноническое разложение этого процесса. В качестве базисных функций j_j(t) должны использоваться координатные функции. Коэффициенты разложения с_k будут искомыми координатами.

В силу сложности нахождения координатных функций указанная процедура не нашла пока применения в инженерной практике. Поэтому идут по пути упрощения модели, предполагая сигнал стационарным или квазистационарным. Некоррелированные координаты, как и ранее, дает только каноническое разложение, однако определение координатных функций упрощается. В качестве таковых могут быть взяты, например, тригонометрические функции. Разложение процесса на ограниченном интервале времени, превышающем длительность корреляции, принимает вид ряда Фурье, но с коэффициентами-координатами, являющимися случайными величинами (1.95). При дискретизации каждой реализации мы будем получать, естественно, детерминированные координаты.

Если отказаться от требования некоррелированности координат, то случайный процесс можно разложить по любой полной системе ортогональных функций. Координатами реализаций будут обобщенные коэффициенты Фурье (см. § 1.3).

Поскольку выражение координат в рассматриваемом случае связано с операцией интегрирования, алгоритмы дискретизации отличаются высокой помехоустойчивостью. Известны примеры успешного использования для целей дискретизации функций Лежандра, Уолша, Хаара. Тем не менее, в силу сложности технической реализации, как получения координат, так и восстановления по ним сигнала, а также вследствие возникновения при этом задержки сигнала во времени методы получения координат на основе «взвешенного» интегрирования сигнала на практике используются лишь иногда при высоком уровне импульсных помех.

Более широкое распространение получили методы дискретизации, при которых сигнал u(t) заменяется совокупностью его мгновенных значений u(t_j), взятых в определенные моменты времени t_j(j=1,2,..., Ν) и называемых выборками или отсчетами. Роль весовых функций (t) в соотношении (2.3) в этом случае выполняют дельта-функции Дирака. В соответствии с (1.11) устанавливаем, что координаты с₁, c₂,..., c_N представляют собой выборки u(t_j)[ξ_j(t) = d(t - t_j)] или разности соседних выборок Δu(t_j) = u(t_j) — u(t — t_j)[x_j(t) = d(t - t_j) - δ(t - t_j-1)].

Поскольку дельта-функция технически нереализуема, длительность каждой выборки конечна. Отсчеты берут не в одной точке, а в некотором интервале времени, зависящем от длительности управляющего импульса ключевого устройства. Когда длительность импульса значительно меньше шага дискретизации, выборки представляют собой короткие импульсы, амплитуды которых пропорциональны мгновенным значениям сигнала.

Отрезок времени t_j = t_j — t_j-1 между соседними выборками называют шагом дискретизации. Если он выдерживается постоянным во всем диапазоне преобразования, дискретизация считается равномерной. Методы равномерной дискретизации получили наиболее широкое применение. Они характеризуются простым алгоритмом, исключающим необходимость фиксировать время отсчетов, что существенно облегчает техническую реализацию. Правда, в этом случае несоответствие шага дискретизации характеру поведения конкретной реализации сигнала на отдельных участках часто приводит к значительной избыточности отсчетов.

Если отрезки времени между выборками меняются, например, в зависимости от скорости изменения сигнала или по заданной программе, дискретизацию называют неравномерной.

В ряде случаев наряду с выборками u(t_j) в качестве координат сигнала используются также производные u(t) в те же моменты времени t_j, вплоть до N-го порядка.

Учитывая теоретическую и практическую значимость методов дискретизации с использованием выборок в качестве координат сигнала, в процессе дальнейшего рассмотрения вопросов дискретизации ограничимся только ими.

§ 2.3. СПОСОБЫ ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНОГО СИГНАЛА

Воспроизведение сигнала по выборкам можно производить как на основе ортогональных, так и неортогональных базисных функций, которые определяют тип аппроксимирующего полинома и принцип приближения: интерполяционный, экстраполяционный, комбинированный.

При неортогональных представлениях сигнала наиболее часто используются степенные алгебраические полиномы вида

или

где α_j — действительные коэффициенты.

Если координаты сигнала представлены в виде разности выборок, то при его восстановлении, как правило, сначала проводят вычисление последовательности выборок и уже по ним строят аппроксимирующий полином u^*(t).

Выбор системы базисных функций в составе аппроксимирующего полинома u*(t) во многом определяется требованием обеспечения простоты технической реализации аппаратных (программных) средств дискретизации и восстановления сигнала.

Если базисные функции выбраны так, что значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим.

С точки зрения сокращения числа отсчетов интерполяционные методы восстановления сигнала предпочтительнее, однако, для их реализации необходима задержка сигнала на интервал интерполяции, что в ряде случаев недопустимо. Поэтому в системах управления, работающих в реальном времени, используются экстра-поляционные методы, не требующие задержки сигнала при проведении операций определения значений выборок и восстановления сигнала.

При замене функции u(t) совокупностью отсчетов основная задача заключается в том, чтобы на интервале преобразования взять их не более чем требуется для восстановления исходного сигнала с заданной точностью в соответствии с выбранным критерием качества приближения.

Ограничение на число членов аппроксимирующего полинома (2.4) обычно не позволяет обеспечить заданную точность воспроизведения на всем интервале преобразования Т. Поэтому его разбивают на отрезки τ_j, называемые участками аппроксимации, и на каждом из них воспроизведение осуществляют аппроксимирующим полиномом (2.4), причем длительность участков аппроксимации может быть различной. В случае использования интерполяционного метода восстановления многочленом ненулевой степени на участке аппроксимации может размещаться несколько отсчетов.

§ 2.4. КРИТЕРИИ КАЧЕСТВА ВОССТАНОВЛЕНИЯ

При известной конечной совокупности координат сигнала и выбранном способе воспроизведения должна обеспечиваться заданная точность восстановления сигнала. Требования к точности восстановления диктуются потребителем информации. В зависимости от целевого назначения получаемой информации используются различные критерии точности приближения u*(t) к u(t).

В соответствии с критерием равномерного воспроизведения, называемым также критерием наибольшего отклонения, устанавливается абсолютное значение допустимой погрешности:

где d_m — максимальная погрешность приближения; Δ_i — участок аппроксимации; d_u(t) = u(t) — u*(t) — текущая погрешность приближения.

Если сигнал задан множеством возможных реализаций, то наибольшая допустимая погрешность 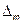устанавливается для всей совокупности реализаций u(t) и

u*(t):

Такой критерий применяется, например, в случаях, когда необходимо обеспечить возможность фиксации любых изменений исходного сигнала, включая кратковременные выбросы, в особенности, если они соответствуют аварийному режиму объекта.

Широко используется также критерий среднеквадратического приближения:

где s_Д — допустимая среднеквадратическая погрешность приближения; σ— среднеквадратическая погрешность приближения.

При множестве возможных реализаций сигнала величина σ усредняется в соответствии с их вероятностями.

В технической реализации неравномерная дискретизация на основе критерия среднеквадратического приближения сложнее, чем на базе критерия равномерного приближения.

Интегральный критерий приближения определяется соотношением

где e_Д - допустимая средняя погрешность приближения; ε — средняя погрешность приближения.

Применяется также вероятностный критерий, в соответствии с которым задается допустимый уровень р_Д величины ρ — вероятности того, что текущая погрешность приближения d(t) не превысит некоторого определенного значения d₀:

§ 2.5. МЕТОДЫ ДИСКРЕТИЗАЦИИ ПОСРЕДСТВОМ ВЫБОРОК

При построении метода дискретизации необходимо сформулировать критерий выбора отсчетов, установить процедуру восстановления по ним исходного сигнала и иметь возможность определить возникающую при этом погрешность. Решение указанных задач возможно лишь на базе выбора определенной математической модели дискретизируемого сигнала.

В вопросе определения величины шага при равномерной дискретизации известно несколько подходов, отличающихся, прежде всего тем, каким параметром характеризуются динамические свойства сигнала.

В теоретических исследованиях наибольшее распространение получила модель сигнала в виде квазистационарного случайного процесса, каждая реализация которого представляет собой функцию с ограниченным спектром. Величина шага дискретизации в этом случае ставится в зависимость от наивысшей частоты спектра. Такой критерий выбора отсчетов принято называть частотным.

При определении шага дискретизации можно ориентироваться непосредственно на степень некоррелированности отсчетов. Существует подход, где за модель

сигнала принят случайный процесс конечной длительности Т, спектр которого отличен от нуля на всей оси частот. В предположении, что t₀<<T, отсчеты берут через интервал корреляции τ₀, определяемый по известной корреляционной функции сигнала. Такой критерий выбора отсчетов называют корреляционным. Учитывая тесную взаимосвязь спектрального и корреляционного методов анализа сигналов, его иногда рассматривают как разновидность частотного критерия. Поскольку использование корреляционного критерия по сравнению с частотным не упрощает теоретических исследований, он не нашел применения в инженерной практике.

Практическую реализацию равномерной дискретизации чаще всего проводят с использованием аппроксимирующих многочленов в общем случае n-й степени. За математическую модель сигнала принимают стационарный случайный процесс, каждая реализация которого представляет собой непрерывную функцию u(t), имеющую (n+1) ограниченных производных. При этом динамические свойства сигнала задаются максимальным во всем интервале преобразования модулем (n+1)-й его производной. Отсчеты выбирают по критерию наибольшего отклонения.

Так как при равномерной дискретизации шаг выбирают, исходя из максимальных значений динамических характеристик сигнала, то на многих участках интервала дискретизации, где мгновенные значения сигнала резко не меняются, он оказывается заниженным, что приводит к избыточности отсчетов.

Эффективное устранение избыточности в отсчетах обеспечивают методы адаптивной неравномерной дискретизации. Длительности шагов дискретизации в этом случае тесно связаны с текущими значениями параметров реализации сигнала. Отсчеты проводятся при достижении выбранной погрешностью восстановления определенного значения, выполняющего здесь роль критерия.

Основные методы дискретизации по выборкам рассмотрим подробнее.

§ 2.6. РАВНОМЕРНАЯ ДИСКРЕТИЗАЦИЯ. ТЕОРЕМА КОТЕЛЬНИКОВА

Дискретизация по частотному критерию. Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром в наиболее четкой форме сформулировано и доказано акад. В. А. Котельниковым в виде теоремы, получившей в отечественной литературе его имя* [11].

Сначала, не касаясь вопроса адекватности выбранной модели реальному сигналу, рассмотрим существо и доказательство теоремы

Теорема Котельникова. Теорема устанавливает принципиальную возможность полного восстановления детерминированной функции с ограниченным спектром по ее отсчетам и указывает предельное значение интервала времени между отсчетами, при которой такое восстановление еще возможно. Она формулируется следующим образом: функция u(t), допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от 0 до F_c = w_c/(2p), полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервалы времени

Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной ее спектра. Только в случае, когда спектр функции безграничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно (корреляционная связь между ними отсутствует). Сокращение высокочастотной части спектра до граничной частоты ω₁ равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими (рис. 2.2, а). При меньших граничных частотах w₂ (рис. 2.2, б) и w₃ (рис. 2.2, в) имеем более сглаженные функции времени. Поскольку значения этих функций в моменты времени u(t₁) и u(t₁+ t) в пределах некоторого интервала Δt не могут изменяться существенно, можно ограничиться значениями функции, взятыми через интервалы Δt (отсчетами).

Д о к а з а т е л ь с т в о. Пусть функции u(t), описывающей передаваемый сигнал, соответствует спектральная характеристика S(jw), причем

где w_c — наибольшая частота спектра u(t).

Используя обратное преобразование Фурье с учетом соотношения (2.13), запишем

Для моментов времени t_n = nΔt = np/w_c, где n — любое целое число, функция u(t) принимает значения

Функцию S(jw) на интервале существования от - w_c до +w_c можно разложить в ряд Фурье по частотам, периодически продолжая ее с периодом 2w_c (рис. 2.3):

где

Сравнивая (2.15) и (2.16), найдем

Выразим теперь S(jw) через отсчеты исходной функции:

Поскольку суммирование ведется как по положительным, так и по отрицательным числам n, знак перед n можно изменить на обратный:

Подставив это значение в (2.14), определим значения исходной функции в любой момент времени:

Учитывая сходимость ряда Фурье, изменим порядок суммирования и интегрирования:

В полученном выражении вычислим интеграл:

Подставив результат в формулу (2.18), окончательно получим

Итак, функция u(t) выражена через ее дискретные значения, взятые в моменты времени t_n = n t = np/w_c.

Так как при любых целых k и n справедливы соотношения

то

Благодаря этому свойству значения функции u(k) в моменты времени tn = n t представляют собой нечто иное, как ее отсчеты.

Представление функции u(t) в виде ряда (2.19) (ряда Котельникова) является частным случаем разложения (1.1). Роль коэффициентов C_k выполняют отсчеты u(n t) функции u(t). Базисными являются функции вида

Они называются функциями отсчетов.

Графики этих функций при n = 0 и n = 1 приведены на рис. 2.4. Каждая функция ψ_n(t) имеет неограниченную протяженность во времени и достигает своего наибольшего значения, равного единице, в момент времени t = n /w_c; относительно этого момента времени она симметрична. В моменты времени t=rp/w_c, где k n, функция обращается в нуль. Все функции ортогональны между собой на бесконечно большом промежутке времени, что легко проверяется путем вычисления интеграла:

Каждую функцию отсчета можно рассматривать как реакцию (отклик) идеального фильтра нижних частот с граничной частотой F_c на дельта-импульс, приходящий в момент времени t_n = n t и имеющий площадь, равную u(n t).

Теорема Котельникова распространяется на непрерывный в среднеквадратическом смысле стационарный случайный процесс с ограниченным энергетическим спектром (S_n(w) = 0 при |ω|>ω_П = 2pF_П).

Такой процесс представляется суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов — величины выборок:

где

Таким образом, при указанных ограничениях случайный процесс полностью определяется счетным множеством случайных величин — координат процесса.

Пример 2.1. Определить по теореме Котельникова шаг дискретизации Δ< для детерминированной функции

ориентируясь на практическую ширину спектра (1.60) с η = 0,95. По формуле (1 42) находим спектральную характеристику

откуда

Практическую ширину спектра определяем, пользуясь соотношением (1.60).

Поскольку

имеем

По таблице значений тангенсов получаем

Следовательно,

§ 2.7. ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ТЕОРЕМЫ КОТЕЛЬНИКОВА

Соотношения (2.19) и (2.23), как и другие разложения функции, имеют прежде всего теоретическое значение и используются при решении различных задач анализа и синтеза систем связи. В частности, они позволили подойти к вопросу передачи непрерывных и дискретных сигналов с единых позиций.

При этом мы оперируем с математическими абстракциями. Бесконечно протяженную во времени функцию (а только такая и может иметь ограниченный спектр) представляем суммой бесконечного числа бесконечно протяженных во времени составляющих функций (функции отсчетов).

Процедура теоретического восстановления конкретной реализации u(t) по ее отсчетам сводится к следующему.

На передающей стороне в исходной непрерывной функции u(t) через интервалы времени Δt определяются мгновенные значения u(n t) и передаются в канал связи в виде δ-импульсов с амплитудами А_n и бесконечно малой длительностью τ, имеющих площади Α_nτ, равные u(nΔt). На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот, у которого частота среза равна F_c. При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал u(t).

Однако использование теоремы как точного утверждения по отношению к реальным сигналам, равно как и попытки организовать на ее основе технический способ дискретной передачи непрерывных сигналов, наталкивается на ряд принципиальных трудностей.

Во-первых, реальный сигнал имеет конечную длительность Т и, следовательно, при представлении его в частотной области обладает неограниченным спектром.

Однако в силу свойств реальных источников сигналов и ограниченности полосы пропускания реальных каналов спектр сигнала с той или иной степенью точности можно считать ограниченным некоторой предельной частотой F_m. Обычно она определяется на основе энергетического критерия. Спектр ограничивается областью частот от 0 до F_m, в которой сосредоточена подавляющая часть энергии сигнала (80—95%). Такое ограничение спектра, естественно, приводит к искажению сигнала.

Относительная точность воспроизведения сигнала γ может быть определена из соотношения

где Р_e — энергия отброшенных высокочастотных составляющих сигнала; Рс — полная энергия сигнала.

Таким образом, восстановление ограниченного во времени сигнала по отсчетам, полученным по теореме Котельникова при условии принудительного ограничения спектра сигнала, возможно только приближенно. Ошибка возникает не только за счет принудительного ограничения спектра, но и за счет конечного числа отсчетов в интервале времени Т, которых в соответствии с теоремой Котельникова будет 2F_cT. Эта составляющая является следствием пренебрежения вкладом бесконечного числа функций отсчета, соответствующих выборкам за пределами интервала Т (рис. 2.5). Погрешность восстановления исходной функции на интервале Т по ограниченному числу членов ряда Котельникова рассматривается, например, в [19].

Модель сигнала с ограниченным спектром имеет еще одно теоретическое неудобство. Она не может отображать основное свойство сигнала — способность нести информацию. Причина — возможность теоретического предсказания поведения функции с ограниченным спектром на всей оси времени, если она точно известна на сколь угодно малом отрезке времени.

Указанные принципиальные трудности устраняются, если рассматривать теорему Котельникова как приближенную для функций с неограниченным спектром.

Во-вторых, предполагаемая процедура восстановления вносит весьма существенную дополнительную погрешность. Она возникает потому, что невозможно обеспечить создание импульсов бесконечно малой длительности, как невозможно осуществить их передачу по реальным каналам связи. Кроме того, максимум выходного сигнала, соответствующего реакции идеального фильтра низких частот на дельта-импульс, запаздывает на время, равное бесконечности. За конечное время Т (рис. 2.5) каждая функция отсчета, а, следовательно, и их сумма, представляющая собой исходный непрерывный сигнал, будут сформированы лишь приближенно и тем грубее, чем меньше Т.

Суммарная погрешность, возникающая при приемлемой сложности средств технической реализации указанного способа передачи, делает его малопригодным для практического использования при восстановлении сигнала даже в случае отсутствия помех в канале связи.

Следует отметить, что в процессе преобразования сигнала в цифровую форму критерий Котельникова используется весьма широко.

§ 2.8. ДИСКРЕТИЗАЦИЯ ПО КРИТЕРИЮ НАИБОЛЬШЕГО ОТКЛОНЕНИЯ

В процессе дискретизации непрерывная функция u(t) имеющая (n+1) ограниченных производных, аппроксимируется многочленом n-й степени. В зависимости от выбранного способа восстановления он может быть интерполирующим или экстраполирующим. Задача обеспечения минимальной погрешности при восстановлении сигнала на практике не ставится. Обычно указывается ее допустимое значение ε₀.

Погрешность восстановления d_u(t) функции u(t) многочленом u*(t) на каждом участке аппроксимации определяется остаточным членом L_n(t):

Следовательно, шаг дискретизации должен быть выбран из условия Ln(t) e₀.

Выбор аппроксимирующего многочлена более высокой степени при малой допустимой погрешности ε₀ обеспечивает меньшее число отсчетов, однако, при этом существенно возрастает сложность технической реализации метода. Поэтому обычно ограничиваются многочленами нулевой, первой и второй степеней (ступенчатая, линейная и параболическая аппроксимации соответственно).

Преимущества и недостатки использования интерполирующих и экстраполирующих многочленов указывались ранее. В качестве интерполирующих чаще других используются многочлены Лагранжа, а в качестве экстраполирующих — многочлены Тейлора.

Дискретизация с использованием интерполирующих многочленов Лагранжа. Интерполирующий многочлен Лагранжа при равномерной дискретизации может быть записан в виде

где

Значение остаточного члена L_n(t)

где M_n+1 — максимальный во всем интервале преобразования модуль (n+1) - й производной сигнала u(t).

Пример 2.2. Определить шаг равномерной дискретизации на основе интерполирующих многочленов Лагранжа нулевой степени.

Значение восстанавливающей функции u*(t) в любой момент времени t на каждом j-м интервале t_j-1 t_j, принимается равным отсчету u(t_j) (рис. 2.6). Соотношение (2.27) позволяет получить выражение для остаточного члена:

Его максимальное значение пропорционально шагу дискретизации. Оно не должно превышать ε₀. Отсюда условие, определяющее шаг дискретизации:

Если проводить восстановление сигнала u(t) по двум отсчетам, пользуясь функциями

то при том же шаге дискретизации погрешность восстановления уменьшится вдвое (рис 2.7).

Пример 2.3. Определим шаг равномерной дискретизации с помощью интерполирующих многочленов Лагранжа первой степени.

При восстановлении исходного сигнала u(t) на каждом интервале времени [t_j-1, t_j] используются два отсчета u(t_j) и u(t_j-1). Они соединяются прямой линией (рис.2.8) Максимальное значение для остаточного члена L найдем, приравняв нулю его производную.

откуда допустимый шаг дискретизации

Дискретизация с использованием экстраполирующих многочленов Тейлора. Экстраполирующий многочлен Тейлора определяется выражением:

где uⁿ(t₀) — n-я производная сигнала U(t) в момент времени t₀.

Поиск по сайту: