Возрастание и убывание функции

Поясним сущность процесса изменения функции графически.

Из геометрии известно, что для острого угла >0, для тупого <0. Так как производная , то на участке 1-2, где >0 - функция возрастает, а на участке 2-3, где , функция убывает.

Таким образом, доказана важная теорема: если производная функции положительна в пределах интервала, то функция у=f(х) на этом интервале возрастает, если производная отрицательна, то функция на интервале убывает.

Особое значение имеет точка 2, в которой касательная параллельна оси оХ и Такие точки называются стационарными и часто характеризуют момент смены возрастания на убывание и наоборот. Этих точек может быть и несколько.

Экстремумы функции

Среди стационарных точек выделим экстремальные: функция имеет максимум (минимум) в точке х=а, если вблизи этой точки всем значениям х соответствуют меньшие (большие), чем . По нашему чертежу точка 2 является точкой экстремума, в данном случае - максимума.

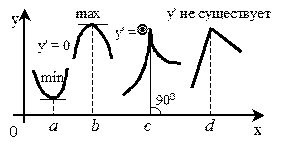
Сформулируем необходимое условие экстремума: если функция имеет экстремум в точке х=а, то в этой точке ее производная либо равна 0, либо бесконечна, либо не существует.

Отметим, что необходимое условие экстремума еще не гарантирует присутствие экстремума. Кроме того, оно не дает ответа о типе экстремума - минимуме или максимуме. И, наконец, оно может соблюдаться и не в экстремальных точках, что и показано на рисунке.

Таким образом, чтобы установить наличие экстремума и определить его тип, следует сформулировать достаточные условия. На практике используют два основных условия:

Первое достаточное условие экстремума: если в стационарной точке х=а производная меняет свой знак с плюса на минус (с возрастания на убывание), то функция у= в этой точке имеет максимум, если с минуса на плюс, то функция имеет минимум.

Первое достаточное условие обычно используют в случаях, когда производная имеет громоздкий вид. Если же вторая производная вычисляется достаточно просто, то удобно использовать следующее условие.

Второе достаточное условие: если в стационарной точке х=а вторая производная положительна, то функция в этой точке имеет минимум, если же отрицательна, то функция имеет максимум.

Таким образом, приведем схему определения экстремумов функции :

· Определяем производную .

· Находим стационарные точки функции из анализа области определения производной и уравнения .

· Выбираем первое или второе достаточное условие. В последнем случае находим

· Исследуем стационарные точки по достаточному условию, определяем наличие и вид экстремума.

· Вычисляем экстремальные значения функции у_экстр.=f(х_стац.).

Заметим, что, если интервал изменения функции ограничен, т.е. то часто возникает задача отыскания наибольшего и наименьшего значений (глобальных экстремумов) функции на этом интервале, причем они могут далеко не всегда совпадать с локальными. Для решения проблемы сравниваются не только внутренние экстремумы, но и проверяются значения функции и на концах интервала. На чертеже показано, что глобальный и локальный минимумы совпадают и равны , но глобальный максимум не совпадает с локальным

Поиск по сайту: