АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос 33. Свойства выборочной дисперсии

Читайте также:
  1. I. Постановка вопроса
  2. IХ. Примерный перечень вопросов к итоговой аттестации
  3. Авторская статья Владимира Путина «Россия: национальный вопрос» (выдержки)
  4. АК. Структура белков, физико-химические свойства (192 вопроса)
  5. Аксиома вторая. Вопрос о производственных отношениях вторичен по отношению к вопросу о типе жизнедеятельности.
  6. Активные минеральные добавки. Смешанные цементы, их свойства.
  7. Альтернативный вопрос (вопрос выбора)
  8. Анализ свойства вязкости
  9. Анализ состояния вопроса
  10. Анамнез и его разделы. Приоритет отечественной медицины в разработке анамнестического метода. Понятие о наводящих вопросах: прямых и косвенных.
  11. Антигены, основные свойства. Антигены гистосовместимости. Процессинг антигенов.
  12. Арифметическая середина и ее свойства.

Эмпирическая дисперсия обладает рядом свойств.

1. Свойство минимальности, которое заключается в том, что эмпирическая дисперсия меньше среднего квадратов отклонений наблюдений от любой точки, не равной средней арифметической.

Данное свойство можно представить в виде следующего выражения: если

Действительно, согласно свойству средней арифметической, сумма квадратов отклонений вариант от их средней арифметической меньше, чем сумма квадратов отклонений от любой другой величины, не равной средней. Если обе части неравенства, выражающего это свойство разделить на объем выборки n получим: для любого Учитывая формулу дисперсии, неравенство можно преобразовать следующим образом: если

2. Дисперсия постоянной величины равна нулю. В самом деле, если все элементы выборки объёма n равны между собой и равны величине c то эмпирическая дисперсия будет равна:

Так как то выражение для дисперсии постоянной величины можно преобразовать следующим образом:

3. Если к каждому наблюдению в выборке прибавить константу c (-¥ < c < ¥), то выборочная дисперсия не изменится. Действительно: Учитывая свойство среднего арифметического и формулу дисперсии, предыдущее выражение можно преобразовать следующим образом:

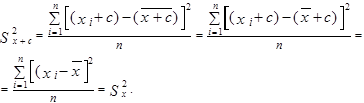
4. Если каждое наблюдение в выборке умножить на константу c (-¥ < c < ¥), то эмпирическая дисперсия увеличится в c 2 раз, то есть: Покажем это. Учитывая свойство среднего арифметического и формулу дисперсии, предыдущее выражение можно преобразовать:

5. Если ряд наблюдений состоит из двух групп, то выборочная дисперсия такого ряда равна сумме средневзвешенной из дисперсий групп и средневзвешенной из квадратов отклонений групповых средних от общей средней. При этом в качестве весов служат объёмы групп.

.

Данное свойство можно обобщить на случай, когда выборка состоит из k групп наблюдений. Чтобы сделать такое обобщение, целесообразно ввести понятия межгрупповой и внутригрупповой дисперсии. Межгрупповой дисперсией называют среднее арифметическое квадратов отклонений групповых средних от средней для всей выборки. Причём, в качестве весов при вычислении этой дисперсии используют объёмы групп.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)