Метод определения расхода

8.3.1 Принцип метода

Расход среды определяют методом переменного перепада давления. Принцип метода состоит в том, что в ИТ, по которому протекает среда, устанавливают СУ, создающее местное сужение потока. Вследствие перехода части потенциальной энергии, потока, в кинетическую, средняя скорость потока, в суженном сечении, повышается. В результате чего статическое давление в этом сечении становится меньше статического давления перед СУ. Разность этих давлений тем больше, чем больше расход протекающей среды, и, следовательно, она может служить мерой расхода.

Из закона сохранения энергии для стационарного потока следует:

(8.7)

Использование в решении этого уравнения условия неразрывности потока несжимаемой среды:

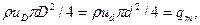(8.8)

приводит к теоретическому уравнению расхода несжимаемой среды:

(8.9)

где u_D– скорость течения потока в ИТ;

u_d– скорость течения потока в отверстии СУ;

Р₁– давление на входе в СУ;

P₂– давление на выходе из СУ;

ρ– плотность несжимаемой жидкости;

E – коэффициент скорости входа.

(8.10)

Δ Р = (Р₁ – P₂) – перепад давления на СУ.

Действительный массовый расход получается меньше рассчитанного по теоретическому уравнению расхода, что корректируется коэффициентом истечения С и дополнительно коэффициентом расширения е для сжимаемых сред. Тогда уравнение расхода принимает вид:

(8.11)

Значения С и ε определены в результате экспериментальных исследований, проведенных на гидравлически гладких трубопроводах при равномерном распределении скоростей потока по сече­нию трубопровода и развитом турбулентном режиме течения этого потока. При исследованиях применяли диафрагмы с острой входной кромкой.

Наличие местных гидравлических сопротивлений (трубопроводной арматуры, отводов и т.д.) и применение шероховатых трубопроводов приводит к искажению распределения скорости по их сечению.

Для выравнивания распределения скоростей по сечению ИТ, неравномерность которого обусловлена наличием местных сопротивлений, применяют прямые участки трубопроводов определенной длины.

Влияние на коэффициент истечения притупления входной кромки отверстий диафрагмы, обусловленного ее износом, корректируют с помощью поправочного коэффициента на притупление входной кромки отверстия диафрагмы.

Таким образом, уравнение массового расхода в общем случае примет вид:

(8.12)

где α = Е С

Введение коэффициентов, учитывающих влияние шероховатости внутренней поверхности ИТ и степени притупления входной кромки диафрагмы, расширяет область применения СУ.

Значение объемного расхода, приведенного к стандартным условиям, может быть определено из уравнения:

(8.13)

Значение объемного расхода в рабочих условиях может быть определено из уравнения:

(8.14)

8.3.2 Расчет коэффициента истечения

В общем случае коэффициент истечения представляют уравнением:

, (8.15)

где C_Re, В и n – параметры, зависящие от типа СУ, причем C_Re = В/С_~

Поправочный коэффициент на число Рейнольдса представляет собой уравнение:

(8.16)

Тогда:

C=C_~ K_Re. (8.17)

Коэффициенты С, В и C_Re зависят только от параметров СУ.

Из уравнений (8.2), (8.3) и (8.6) видно, что С и K_Rе зависят от числа Ренольдса, число Рейнольдса зависит от значения расхода, а значение расхода, в свою очередь, зависит от С и K_Re

Алгоритм определения расхода можно упростить без изменения погрешности определения С, если уравнение (8.6) представить в виде:

, (8.18)

где Re_~ – число Рейнольдса, найденное для расхода, определенного

при С = С_~;

а и b – постоянные коэффициенты, зависящие от типа СУ (разделы 8 – 10 ГОСТ Р 8. 563.1). Значения коэффициентов а и b получают из уравнения:

(8.19)

Уравнение (8.19) – результат линейной аппроксимации К^-n_Re от К_Re для СУ каждого типа.

В связи с тем, что изменение значения K_Re лежит в небольших пределах (менее ±4 %), а значения K_Re и n близки к единице, аппроксимация К^-n_Re является достаточно точной и не влияет на погрешность определения коэффициента истечения.

8.3.3 Порядок определения массового расхода

Порядок определения массового расхода сводится к следующей процедуре:

- определяют β;

- определяют С_~;

- при выполнении условия для диафрагм и условия для сопел ИСА 1932 и сопел Вентури коэффициент шероховатости К_ш принимают равным единице; при невыполнении указан­ных условий определяют приближенное значение коэффициента шероховатости К_ш принимая A_Rе = 0,5;

- вычисляют массовый расход при С= С_~, т.е. q_m~ по уравнению:

(8.20)

- рассчитывают Re при массовом расходе q_m~, т. е. по уравнению:

(8.21)

определяют K_Rе по уравнению (8.18); определяют число Рейнольдса по уравнению:

(8.22)

- при выполнении условия для диафрагм, для сопел ИСА 1932 и сопел Вентури (K_ш=1) определяют действительное значение массового расхода по уравнению:

(8.23)

- при невыполнении условия для диафрагм рассчитывают действительное значение коэффициента шероховатости K_ш' с учетом зависимости от Re; в этом случае действительное значение массового расхода определяют по:

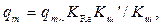(8.24)

Поиск по сайту: